【题目】已知函数f（x）=ex+ax，（a∈R），其图象与x轴交于A（x1 ， 0），B（x2 ， 0）两点，且x1＜x2
（1）求a的取值范围；
（2）证明： ；（f′（x）为f（x）的导函数）
（3）设点C在函数f（x）的图象上，且△ABC为等边三角形，记 ，求（t﹣1）（a+ ）的值．

【题目】已知椭圆C： =1（a＞b＞0）的离心率为 ，F1、F2分别是椭圆的左、右焦点，M为椭圆上除长轴端点外的任意一点，且△MF1F2的周长为4+2 ．
（1）求椭圆C的方程；
（2）过点D（0，﹣2）作直线l与椭圆C交于A、B两点，点N满足 （O为原点），求四边形OANB面积的最大值，并求此时直线l的方程．

【题目】某校后勤处为跟踪调查该校餐厅的当月的服务质量，兑现奖惩，从就餐的学生中随机抽出100位学生对餐厅服务质量打分(5分制)，得到如下柱状图：

（1）从样本中任意选取2名学生，求恰好有一名学生的打分不低于4分的概率；
（2）若以这100人打分的频率作为概率，在该校随机选取2名学生进行打分(学生打分之间相互独立)记 表示两人打分之和，求 的分布列和 .

【题目】已知圆C1的圆心在坐标原点O，且恰好与直线相切．

(Ⅰ)求圆C1的标准方程；

(Ⅱ)设点A为圆上一动点，AN垂直于x轴于点N，若动点Q满足

(其中m为非零常数)，试求动点Q的轨迹方程；

(Ⅲ)在(Ⅱ)的结论下，当m＝时，得到动点Q的轨迹为曲线C，与l1垂直的直线l与曲线C交于B，D两点，求△OBD面积的最大值．

【题目】函数 .
（1）求函数 的最小正周期；
（2）在 中， 分别为内角 的对边，且 ， ，求 的面积的最大值.

【题目】设 方程 有两个不等的负根， 方程 无实根，若“ ”为真，“ ”为假，求实数 的取值范围.

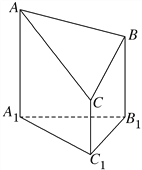
(Ⅰ)该几何体的体积；

(Ⅱ)截面ABC的面积．

【题目】命题 ：关于 的不等式 对一切 恒成立，命题 ：指数函数 是增函数，若 或 为真、 且 为假，求实数 的取值范围.

【题目】某公司在迎新年晚会上举行抽奖活动，有甲、乙两个抽奖方案供员工选择；
方案甲：员工最多有两次抽奖机会，每次抽奖的中奖率为 .第一次抽奖，若未中奖，则抽奖结束.若中奖，则通过抛一枚质地均匀的硬币，决定是否继续进行第二次抽奖，规定：若抛出硬币，反面朝上，员工则获得500元奖金，不进行第二次抽奖；若正面朝上，员工则须进行第二次抽奖，且在第二次抽奖中，若中奖，获得奖金1000元；若未中奖，则所获奖金为0元.
方案乙：员工连续三次抽奖，每次中奖率均为 ，每次中奖均可获奖金400元.
（1）求某员工选择方案甲进行抽奖所获奖金 （元）的分布列；
（2）某员工选择方案乙与选择方案甲进行抽奖，试比较哪个方案更划算？

【题目】一个正四面体的“骰子”（四个面分别标有1，2，3，4四个数字），掷一次“骰子”三个侧面的数字的和为“点数”，连续抛掷“骰子”两次．
（1）设A为事件“两次掷‘骰子’的点数和为16”，求事件A发生的概率；
（2）设X为两次掷“骰子”的点数之差的绝对值，求随机变量X的分布列和数学期望．