
科目: 来源: 题型:
【题目】已知![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]() 为偶函数,对于函数
为偶函数,对于函数![]() 有下列几种描述:
有下列几种描述:
①![]() 是周期函数; ②
是周期函数; ②![]() 是它的一条对称轴;
是它的一条对称轴;
③![]() 是它图象的一个对称中心; ④当
是它图象的一个对称中心; ④当![]() 时,它一定取最大值;
时,它一定取最大值;
其中描述正确的是__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】共享单车是城市交通的一道亮丽的风景,给人们短距离出行带来了很大的方便.某校”单车社团”对![]() 市年龄在
市年龄在![]() 岁骑过共享单车的人群随机抽取
岁骑过共享单车的人群随机抽取![]() 人调查,骑行者的年龄情况如下图显示。
人调查,骑行者的年龄情况如下图显示。
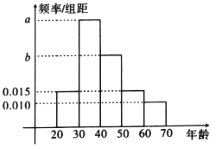
(1)已知![]() 年龄段的骑行人数是
年龄段的骑行人数是![]() 两个年龄段的人数之和,请估计骑过共享单车人群的年齡的中位数;
两个年龄段的人数之和,请估计骑过共享单车人群的年齡的中位数;
(2)从![]() 两个年龄段骑过共享单车的人中按
两个年龄段骑过共享单车的人中按![]() 的比例用分层抽样的方法抽取
的比例用分层抽样的方法抽取![]() 人,从中任选
人,从中任选![]() 人,求两人都在
人,求两人都在![]() )的概率.
)的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率
的离心率![]() ,左顶点为
,左顶点为![]() ,过点
,过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.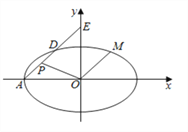
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() 为
为![]() 的中点,是否存在定点
的中点,是否存在定点![]() ,对于任意的
,对于任意的![]() 都有
都有![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)若过![]() 点作直线
点作直线![]() 的平行线交椭圆
的平行线交椭圆![]() 于点
于点![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知以M为圆心的圆M: ![]() 及其上一点A(2,4)
及其上一点A(2,4)

(1)设圆N与x轴相切,与圆M外切,且圆心N在直线x=6上,求圆N的标准方程;
(2)设平行于OA的直线l与圆M相交于B、C两点,且BC=OA,求直线l的方程;
(3)设点T(t,o)满足:存在圆M上的两点P和Q,使得![]() ,求实数t的取值范围。
,求实数t的取值范围。
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在三棱锥![]() 中,已知
中,已知![]() 是正三角形,
是正三角形, ![]() 平面
平面![]() 为
为![]() 的中点,
的中点, ![]() 在棱
在棱![]() 上,且
上,且![]() .
.
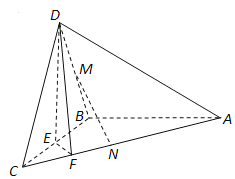
(1)求三棱锥![]() 的体积;
的体积;
(2)求证: ![]() 平面
平面![]() ;
;
(3)若![]() 为
为![]() 中点,
中点, ![]() 在棱
在棱![]() 上,且
上,且![]() ,求证:
,求证: ![]() 平面
平面![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】网购已经成为一种时尚,商家为了鼓励消费,购买时在店铺领取优惠券,买后给予好评返还现金等促销手段.经统计,近五年某店铺用于促销的费用![]() (万元)与当年度该店铺的销售收人
(万元)与当年度该店铺的销售收人![]() (万元)的数据如下表:
(万元)的数据如下表:
年份 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 |
促销费用 |
|
|
|
|
|
销售收入 |
|
|
|
|
|
(1)请根据上表提供的数据,用最小二乘法求出/span>![]() 关于
关于![]() 的线性回归方
的线性回归方![]() ;
;
(2)2018年度该店铺预测销售收人至少达到![]() 万元,则该店铺至少准备投入多少万元的促销费?
万元,则该店铺至少准备投入多少万元的促销费?
参考公式: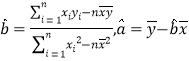
参考数据: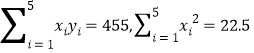
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,过底面是矩形的四棱锥FABCD的顶点F作EF∥AB,使AB=2EF,且平面ABFE⊥平面ABCD,若点G在CD上且满足DG=G![]() .
.

求证:(1)FG∥平面AED;
(2)平面DAF⊥平面BAF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com