
科目: 来源: 题型:
【题目】某校高二年级进行了百科知识大赛,为了了解高二年级900名同学的比赛情况,现在甲、乙两个班级各随机抽取了10名同学的成绩,比赛成绩满分为100分,80分以上可获得二等奖,90分以上可以获得一等奖,已知抽取的两个班学生的成绩(单位:分)数据的茎叶图如图1所示:

(1)比较两组数据的分散程度(只需要给出结论),并求出甲组数据的频率分布直方图如图2中所示的![]() 值;
值;
(2)现从两组数据中获奖的学生里分别随机抽取一人接受采访,求被抽中的甲班学生成绩高于乙班学生成绩的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点,
的中点, ![]() 是
是![]() 与
与![]() 的交点,将
的交点,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,如图2.
的位置,如图2.
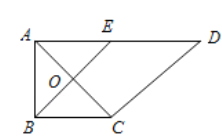

图1 图2
(1)证明: ![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1所示,在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的平分线,点
的平分线,点![]() 在线段
在线段![]() 上,
上, ![]() .如图2所示,将
.如图2所示,将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() ,连结
,连结![]() ,设点
,设点![]() 是
是![]() 的中点.
的中点.
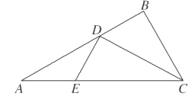

图1 图2
(1)求证: ![]() 平面
平面![]() ;
;
(2)在图2中,若![]() 平面
平面![]() ,其中
,其中![]() 为直线
为直线![]() 与平面
与平面![]() 的交点,求三棱锥
的交点,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校高二年级进行了百科知识大赛,为了了解高二年级900名同学的比赛情况,现在甲、乙两个班级各随机抽取了10名同学的成绩,比赛成绩满分为100分,80分以上可获得二等奖,90分以上可以获得一等奖,已知抽取的两个班学生的成绩(单位:分)数据的茎叶图如图1所示:

(1)比较两组数据的分散程度(只需要给出结论),并求出甲组数据的频率分布直方图如图2中所示的![]() 值;
值;
(2)现从两组数据中获奖的学生里分别随机抽取一人接受采访,求被抽中的甲班学生成绩高于乙班学生成绩的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】过点![]() 的直线与圆
的直线与圆![]() 相切,且与直线
相切,且与直线![]() 垂直,则
垂直,则![]() ( )
( )
A. 2 B. 1 C. ![]() D.
D. ![]()
【答案】A
【解析】因为点P(2,2)满足圆![]() 的方程,所以P在圆上,
的方程,所以P在圆上,
又过点P(2,2)的直线与圆![]() 相切,且与直线axy+1=0垂直,
相切,且与直线axy+1=0垂直,
所以切点与圆心连线与直线axy+1=0平行,
所以直线axy+1=0的斜率为: ![]() .
.
故选A.
点睛:对于直线和圆的位置关系的问题,可用“代数法”或“几何法”求解,直线与圆的位置关系体现了圆的几何性质和代数方法的结合,“代数法”与“几何法”是从不同的方面和思路来判断的,解题时不要单纯依靠代数计算,若选用几何法可使得解题过程既简单又不容易出错.
【题型】单选题
【结束】
23
【题目】设![]() 分别是双曲线
分别是双曲线![]() 的左、右焦点.若点
的左、右焦点.若点![]() 在双曲线上,且
在双曲线上,且![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】《九章算术》是我国古代著名数学经典.其中对勾股定理的论术比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深1寸,锯道长1尺.问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示(阴影部分为镶嵌在墙体内的部分).已知弦![]() 尺,弓形高
尺,弓形高![]() 寸,估算该木材镶嵌在墙中的体积约为( )
寸,估算该木材镶嵌在墙中的体积约为( )
(注:1丈=10尺=100寸, ![]() ,
, ![]() )
)

A. 633立方寸 B. 620立方寸 C. 610立方寸 D. 600立方寸
查看答案和解析>>
科目: 来源: 题型:
【题目】过点![]() 的直线与圆
的直线与圆![]() 相切,且与直线
相切,且与直线![]() 垂直,则
垂直,则![]() ( )
( )
A. 2 B. 1 C. ![]() D.
D. ![]()
【答案】A
【解析】因为点P(2,2)满足圆![]() 的方程,所以P在圆上,
的方程,所以P在圆上,
又过点P(2,2)的直线与圆![]() 相切,且与直线axy+1=0垂直,
相切,且与直线axy+1=0垂直,
所以切点与圆心连线与直线axy+1=0平行,
所以直线axy+1=0的斜率为: ![]() .
.
故选A.
点睛:对于直线和圆的位置关系的问题,可用“代数法”或“几何法”求解,直线与圆的位置关系体现了圆的几何性质和代数方法的结合,“代数法”与“几何法”是从不同的方面和思路来判断的,解题时不要单纯依靠代数计算,若选用几何法可使得解题过程既简单又不容易出错.
【题型】单选题
【结束】
23
【题目】设![]() 分别是双曲线
分别是双曲线![]() 的左、右焦点.若点
的左、右焦点.若点![]() 在双曲线上,且
在双曲线上,且![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在三棱锥![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,若该三棱锥的四个顶点均在同一球面上,则该球的体积为( )
,若该三棱锥的四个顶点均在同一球面上,则该球的体积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】在三棱锥![]() 中,因为
中,因为![]() ,
, ![]() ,
, ![]() ,所以
,所以![]() ,则该几何体的外接球即为以
,则该几何体的外接球即为以![]() 为棱长的长方体的外接球,则
为棱长的长方体的外接球,则![]() ,其体积为
,其体积为![]() ;故选D.
;故选D.
点睛:在处理几何体的外接球问题,往往将所给几何体与正方体或长方体进行联系,常用补体法补成正方体或长方体进行处理,本题中由数量关系可证得![]()
![]() 从而几何体的外接球即为以
从而几何体的外接球即为以![]() 为棱长的长方体的外接球,也是处理本题的技巧所在.
为棱长的长方体的外接球,也是处理本题的技巧所在.
【题型】单选题
【结束】
21
【题目】已知函数![]() ,则
,则![]() 的大致图象为( )
的大致图象为( )
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com