
科目: 来源: 题型:
【题目】某厂家举行大型的促销活动,经测算某产品当促销费用为![]() 万元时,销售量
万元时,销售量![]() 万件满足
万件满足![]() (其中
(其中![]() ,
, ![]() 为正常数),现假定生产量与销售量相等,已知生产该产品
为正常数),现假定生产量与销售量相等,已知生产该产品![]() 万件还需投入成本
万件还需投入成本![]() 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为![]() 万元/万件.
万元/万件.
(1)将该产品的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数;
万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点![]() 是直线
是直线![]() (
(![]() )上一动点,
)上一动点, ![]() 、
、![]() 是圆
是圆![]() :
: ![]() 的两条切线,
的两条切线, ![]() 、
、![]() 为切点,
为切点, ![]() 为圆心,若四边形
为圆心,若四边形![]() 面积的最小值是
面积的最小值是![]() ,则
,则![]() 的值是( )
的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】∵圆的方程为: ![]() ,
,
∴圆心C(0,1),半径r=1.
根据题意,若四边形面积最小,当圆心与点P的距离最小时,即距离为圆心到直线l的距离最小时,切线长PA,PB最小。切线长为4,
∴![]() ,
,
∴圆心到直线l的距离为![]() .
.
∵直线![]() (
(![]() ),
),
∴![]() ,解得
,解得![]() ,由
,由![]()
所求直线的斜率为![]()
故选D.
【题型】单选题
【结束】
19
【题目】抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,经过
,经过![]() 且斜率为
且斜率为![]() 的直线与抛物线在
的直线与抛物线在![]() 轴上方的部分相交于点
轴上方的部分相交于点![]() ,
, ![]() ,垂足为
,垂足为![]() ,则
,则![]() 的面积是 ( )
的面积是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】若圆![]() (
(![]() )上仅有
)上仅有![]() 个点到直线
个点到直线![]() 的距离为
的距离为![]() ,则实数
,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】圆心到直线![]() 距离为
距离为![]() ,所以要有
,所以要有![]() 个点到直线
个点到直线![]() 的距离为
的距离为![]() ,需
,需![]() ,选B.
,选B.
点睛:与圆有关的长度或距离的最值问题的解法.一般根据长度或距离的几何意义,利用圆的几何性质数形结合求解.
【题型】单选题
【结束】
15
【题目】设![]() 和
和![]() 为双曲线
为双曲线![]() 的两个焦点,若
的两个焦点,若![]() ,
, ![]() ,
, ![]() 是正三角形的三个顶点,则双曲线的渐近线方程是( )
是正三角形的三个顶点,则双曲线的渐近线方程是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() ,直线
,直线![]() 过抛物线焦点,且与抛物线交于
过抛物线焦点,且与抛物线交于![]() ,
, ![]() 两点,以线段
两点,以线段![]() 为直径的圆与抛物线准线的位置关系是( )
为直径的圆与抛物线准线的位置关系是( )
A. 相离 B. 相交 C. 相切 D. 不确定
查看答案和解析>>
科目: 来源: 题型:
【题目】在棱长为1的正方体![]() 中,点
中,点![]() ,
, ![]() 分别是侧面
分别是侧面![]() 与底面
与底面![]() 的中心,则下列命题中错误的个数为( )
的中心,则下列命题中错误的个数为( )
①![]() 平面
平面![]() ; ②异面直线
; ②异面直线![]() 与
与![]() 所成角为
所成角为![]() ;
;
③![]() 与平面
与平面![]() 垂直; ④
垂直; ④![]() .
.
A. 0 B. 1 C. 2 D. 3
【答案】A
【解析】对于①,∵DF![]() ,DF
,DF![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,正确;
,正确;
对于②,∵DF![]() ,∴异面直线
,∴异面直线![]() 与
与![]() 所成角即异面直线
所成角即异面直线![]() 与
与![]() 所成角,△
所成角,△![]() 为等边三角形,故异面直线
为等边三角形,故异面直线![]() 与
与![]() 所成角为
所成角为![]() ,正确;
,正确;
对于③,∵![]() ⊥
⊥![]() ,
, ![]() ⊥CD,且
⊥CD,且![]() CD=D,∴
CD=D,∴![]() ⊥平面
⊥平面![]() ,即
,即![]() ⊥平面
⊥平面![]() 正确;
正确;
对于④,![]() ,正确,
,正确,
故选:A
【题型】单选题
【结束】
8
【题目】已知函数![]() 在区间
在区间![]() 上单调递增,则实数
上单调递增,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,且
,且![]() ,设命题p:函数
,设命题p:函数![]() 在
在![]() 上单调递减;命题q:函数
上单调递减;命题q:函数![]() 在
在![]() 上为增函数,
上为增函数,
(1)若“p且q”为真,求实数c的取值范围
(2)若“p且q”为假,“p或q”为真,求实数c的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是棱
是棱![]() 上一点.
上一点.
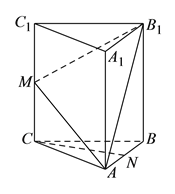
(I)求证: ![]() .
.
(II)若![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() .
.
(III)若二面角![]() 的大小为
的大小为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com