
科目: 来源: 题型:
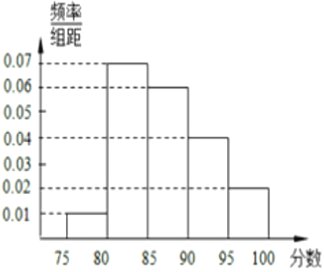
【题目】某高校在今年的自主招生考试成绩中随机抽取 100 名考生的笔试成绩,分为 5 组制出频率分布直方图如图所示.
组号 | 分组 | 频数 | 频率 |
1 |
| 5 | 0.05 |
2 |
| 35 | 0.35 |
3 |
|
|
|
4 |
|
|
|
5 |
| 10 | 0.1 |
(1)求![]() 的值.
的值.
(2)该校决定在成绩较好的 、4、5 组用分层抽样抽取 6 名学生进行面试,则每组应各抽多少名学生?
(3)在(2)的前提下,从抽到 6 名学生中再随机抽取 2 名被甲考官面试,求这 2 名学生来自同一组的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.
(1)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(2)若从亚洲国家和欧洲国家中各选1个,求这两个国家包括A1,但不包括B1的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在半径为![]() ,圆心角为
,圆心角为![]() 的扇形金属材料中剪出一个长方形
的扇形金属材料中剪出一个长方形![]() ,并且
,并且![]() 与
与![]() 的平分线
的平分线![]() 平行,设
平行,设![]() .
.

(1)试将长方形![]() 的面积
的面积![]() 表示为
表示为![]() 的函数;
的函数;
(2)若将长方形![]() 弯曲,使
弯曲,使![]() 和
和![]() 重合焊接制成圆柱的侧面,当圆柱侧面积最大时,求圆柱的体积(假设圆柱有上下底面);为了节省材料,想从△
重合焊接制成圆柱的侧面,当圆柱侧面积最大时,求圆柱的体积(假设圆柱有上下底面);为了节省材料,想从△![]() 中直接剪出一个圆面作为圆柱的一个底面,请问是否可行?并说明理由.
中直接剪出一个圆面作为圆柱的一个底面,请问是否可行?并说明理由.
(参考公式:圆柱体积公式![]() .其中
.其中![]() 是圆柱底面面积,
是圆柱底面面积,![]() 是圆柱的高;等边三角形内切圆半径
是圆柱的高;等边三角形内切圆半径![]() .其中
.其中![]() 是边长)
是边长)
查看答案和解析>>
科目: 来源: 题型:
【题目】某县城出租车的收费标准是:起步价是![]() 元(乘车不超过
元(乘车不超过![]() 千米);行驶
千米);行驶![]() 千米后,每千米车费1.2元;行驶
千米后,每千米车费1.2元;行驶![]() 千米后,每千米车费1.8元.
千米后,每千米车费1.8元.
(1)写出车费与路程的关系式;
(2)一顾客计划行程![]() 千米,为了省钱,他设计了三种乘车方案:
千米,为了省钱,他设计了三种乘车方案:
①不换车:乘一辆出租车行![]() 千米;
千米;
②分两段乘车:先乘一辆车行![]() 千米,换乘另一辆车再行
千米,换乘另一辆车再行![]() 千米;
千米;
③分三段乘车:每乘![]() 千米换一次车.
千米换一次车.
问哪一种方案最省钱.
查看答案和解析>>
科目: 来源: 题型:
【题目】以下四个命题,其中正确的是( )
A. 由独立性检验可知,有 99%的把握认为物理成绩与数学成绩有关,某人数学成绩优秀,则他有 99%的可能物理优秀;
B. 两个随机变量相关系越强,则相关系数的绝对值越接近于 0;
C. 在线性回归方程![]() 中,当变量
中,当变量![]() 每增加一十单位时,变量
每增加一十单位时,变量![]() 平均增加 0.2 个单位;
平均增加 0.2 个单位;
D. 线性回归方程对应的直线![]() 至少经过其样本数据点中的一个点.
至少经过其样本数据点中的一个点.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知曲线![]() 所围成封闭图形面积为
所围成封闭图形面积为![]() ,曲线
,曲线![]() 是以曲线
是以曲线![]() 与坐标轴的交点为顶点的椭圆, 离心率为
与坐标轴的交点为顶点的椭圆, 离心率为![]() . 平面上的动点
. 平面上的动点![]() 为椭圆
为椭圆![]() 外一点,且过
外一点,且过![]() 点
点
引椭圆![]() 的两条切线互相垂直.
的两条切线互相垂直.
(1)求曲线![]() 的方程;
的方程;
(2)求动点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司“Mobike”计划在甲、乙两座城市共投资120万元,根据行业规定,每个城市至少要投资40万元,由前期市场调研可知:甲城市收益P与投入![]() (单位:万元)满足
(单位:万元)满足![]() ,乙城市收益Q与投入
,乙城市收益Q与投入![]() (单位:万元)满足
(单位:万元)满足![]() ,设甲城市的投入为
,设甲城市的投入为![]() (单位:万元),两个城市的总收益为
(单位:万元),两个城市的总收益为![]() (单位:万元).
(单位:万元).
(1)当甲城市投资50万元时,求此时公司总收益;
(2)试问如何安排甲、乙两个城市的投资,才能使总收益最大?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,若在定义域内存在
,若在定义域内存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 为函数
为函数![]() 的局部对称点.
的局部对称点.
(1)若![]() ,证明:函数
,证明:函数![]() 必有局部对称点;
必有局部对称点;
(2)若函数![]() 在区间
在区间![]() 内有局部对称点,求实数
内有局部对称点,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 在
在![]() 上有局部对称点,求实数
上有局部对称点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
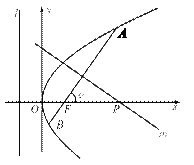
【题目】已知抛物线![]() 上一点
上一点![]() 到焦点
到焦点![]() 的距离
的距离![]() ,倾斜角
,倾斜角
为![]() 的直线经过焦点
的直线经过焦点![]() ,且与抛物线交于
,且与抛物线交于![]() 、
、![]() 两点.
两点.
(1)求抛物线的标准方程及准线![]() 的方程;
的方程;
(2)若![]() 为锐角,作线段
为锐角,作线段![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 轴于点
轴于点![]() ,证明
,证明![]() 为定值,并求此定值.
为定值,并求此定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com