
科目: 来源: 题型:
【题目】对于函数![]() 与常数
与常数![]() ,若
,若![]() 恒成立,则称
恒成立,则称![]() 为函数
为函数![]() 的一个“P数对”,设函数
的一个“P数对”,设函数![]() 的定义域为
的定义域为![]() ,且
,且![]() 。
。
(1)若![]() 是
是![]() 的一个“P数对”,且
的一个“P数对”,且![]() ,求常数
,求常数![]() 的值;
的值;
(2)若(1,1)是![]() 的一个“P数对”,且
的一个“P数对”,且![]() 在
在![]() 上单调递增,求函数
上单调递增,求函数![]() 在
在![]() 上的最大值与最小值;
上的最大值与最小值;
(3)若(-2,0)是![]() 的一个“P数对”,且当
的一个“P数对”,且当![]() 时,
时,![]() ,求k的值及
,求k的值及![]() 在区间
在区间![]() 上的最大值与最小值。
上的最大值与最小值。
查看答案和解析>>
科目: 来源: 题型:
【题目】已知指数函数y=g(x)满足:g(3)=8,定义域为R的函数f(x)=![]() 是奇函数.
是奇函数.
(1)确定y=f(x)和y=g(x)的解析式;
(2)判断函数f(x)的单调性,并用定义证明;
(3)若对于任意x∈[-5,-1],都有f(1-x)+f(1-2x)>0成立,求x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一隧道内设双行线路,其截面由一长方形和一抛物线构成。为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部(抛物线)在竖直方向上的高度之差至少为0.5m,若行车道总宽度AB为6m,请计算通过隧道的车辆的限制高度(精确度为0.1m)
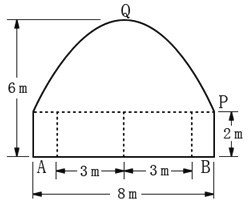
查看答案和解析>>
科目: 来源: 题型:
【题目】已知y=f(x)为二次函数,若y=f(x)在x=2处取得最小值﹣4,且y=f(x)的图象经过原点,
(1)求f(x)的表达式;
(2)求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在四棱锥P﹣ABCD中,底面ABCD是一直角梯形,BA⊥AD,AD∥BC,AB=BC=2,PA=3,PA⊥底面ABCD,E是棱PD上异于P,D的动点.设 ![]() =m,则“0<m<2”是三棱锥C﹣ABE的体积不小于1的( )
=m,则“0<m<2”是三棱锥C﹣ABE的体积不小于1的( ) 
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)已知全集U={2,4,a2-a+1},A={a+4,4},UA={7},则a=________.
(2)当a>0且a≠1时,函数![]() 必过定点_______
必过定点_______
(3)为了保证信息安全,传输必须使用加密方式,有一种方式其加密、解密原理如下:
明文![]() 密文
密文![]() 密文
密文![]() 明文
明文
己知加密为y=ax-2(x为明文、y为密文),如果明文“3”通过加密后得到密文为“6”,再发送,接收方通过解密得到明文“3”,若接收方接到密文为“14”,则原发的明文是________.
(4)已知3a=5b=M,且![]() ,则M的值为______________。
,则M的值为______________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com