【题目】设斜率为2的直线l，过双曲线的右焦 点，且与双曲线的左、右两支分别相交，则双曲线离心率，e的取值范围是 （ ）

A. e＞ B. e＞ C. 1＜e＜ D. 1＜e＜

【题目】已知椭圆的中心在原点，焦点、在轴上，离心率为，在椭圆上有一动点与、的距离之和为4，

(Ⅰ) 求椭圆E的方程；

(Ⅱ) 过、作一个平行四边形，使顶点、、、都在椭圆上，如图所示.判断四边形能否为菱形，并说明理由.

【题目】为了研究某种农作物在特定温度下（要求最高温度满足：）的生长状况，某农学家需要在十月份去某地进行为期十天的连续观察试验．现有关于该地区10月份历年10月份日平均最高温度和日平均最低温度（单位：）的记录如下：

（Ⅰ）根据本次试验目的和试验周期，写出农学家观察试验的起始日期．

（Ⅱ）设该地区今年10月上旬（10月1日至10月10日）的最高温度的方差和最低温度的方差分别为，估计的大小？（直接写出结论即可）．

（Ⅲ）从10月份31天中随机选择连续三天，求所选3天每天日平均最高温度值都在[27，30]之间的概率．

【题目】已知椭圆方程为，它的一个顶点为，离心率.

（1）求椭圆的方程；

（2）设直线与椭圆交于， 两点，坐标原点到直线的距离为，求面积的最大值.

【题目】如图1，在高为2的梯形中， ， ， ，过、分别作， ，垂足分别为、。已知，将梯形沿、同侧折起，得空间几何体，如图2。

（1）若，证明： ；

（2）若，证明： ；

（3）在（1），（2）的条件下，求三棱锥的体积。

【题目】已知函数f（ ）=﹣ x3+ x2﹣m，g（x）=﹣ x3+mx2+（a+1）x+2xcosx﹣m．
（1）若曲线y=f（x）仅在两个不同的点A（x1 ， f（x1）），B（x1 ， f（x2））处的切线都经过点（2，t），求证：t=3m﹣8，或t=﹣ m3+ m2﹣m．
（2）当x∈[0，1]时，若f（x）≥g（x）恒成立，求a的取值范围．

（1）要在这五名学生中选2名参加一项活动，求选中的同学中至少有一人的物理成绩高于90分的概率.

（2）求出这些数据的线性回归直线方程.

参考公式回归直线的方程是： ，

其中对应的回归估计值. ， .

【题目】已知焦距为2的椭圆W： =1（a＞b＞0）的左、右焦点分别为A1 ， A2 ， 上、下顶点分别为B1 ， B2 ， 点M（x0 ， y0）为椭圆W上不在坐标轴上的任意一点，且四条直线MA1 ， MA2 ， MB1 ， MB2的斜率之积为 ．

（1）求椭圆W的标准方程；
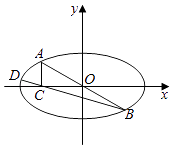
（2）如图所示，点A，D是椭圆W上两点，点A与点B关于原点对称，AD⊥AB，点C在x轴上，且AC与x轴垂直，求证：B，C，D三点共线．

【题目】如图，在四棱锥P﹣ABCD中，侧面PAB⊥底面ABCD，△PAB为正三角形．AB⊥AD，CD⊥AD，点E、M为线段BC、AD的中点，F，G分别为线段PA，AE上一点，且AB=AD=2，PF=2FA．
（1）确定点G的位置，使得FG∥平面PCD；
（2）试问：直线CD上是否存在一点Q，使得平面PAB与平面PMQ所成锐二面角的大小为30°，若存在，求DQ的长；若不存在，请说明理由．

【题目】已知向量,若函数的最小正周期为，且在上单调递减.

(1)求的解析式；

(2)若关于的方程在有实数解，求的取值范围.