
科目: 来源: 题型:
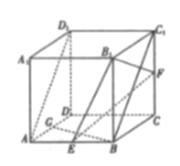
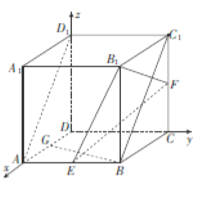
【题目】如图,在正方体![]() 中,
中, ![]() 分别是棱
分别是棱![]() 的中点,
的中点, ![]() 为棱
为棱![]() 上一点,且异面直线
上一点,且异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
(1)证明: ![]() 为
为![]() 的中点;
的中点;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)以![]() 为坐标原点,建立如图所示的空间直角坐标系
为坐标原点,建立如图所示的空间直角坐标系![]() ,不妨令正方体的棱长为2,设
,不妨令正方体的棱长为2,设![]() ,利用
,利用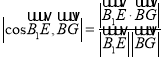 ,解得
,解得![]() ,即可证得;
,即可证得;
(2)分别求得平面![]() 与平面
与平面![]() 的法向量
的法向量![]() ,利用
,利用![]() 求解即可.
求解即可.
试题解析:
(1)证明:以![]() 为坐标原点,建立如图所示的空间直角坐标系
为坐标原点,建立如图所示的空间直角坐标系![]() .
.
不妨令正方体的棱长为2,
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
设![]() ,则
,则![]() ,
, ![]() ,
,
所以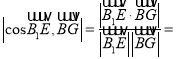
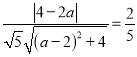 ,
,
所以![]() ,解得
,解得![]() (
(![]() 舍去),即
舍去),即![]() 为
为![]() 的中点.
的中点.
(2)解:由(1)可得![]() ,
, ![]() ,
,
设![]() 是平面
是平面![]() 的法向量,
的法向量,
则![]() .令
.令![]() ,得
,得![]() .
.
易得平面![]() 的一个法向量为
的一个法向量为![]() ,
,
所以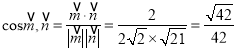 .
.
所以所求锐二面角的余弦值为![]() .
.
点睛:空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.
【题型】解答题
【结束】
22
【题目】已知椭圆![]() 的短轴长为2,且椭圆
的短轴长为2,且椭圆![]() 过点
过点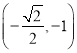 .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 过定点
过定点![]() ,且斜率为
,且斜率为![]() ,若椭圆
,若椭圆![]() 上存在
上存在![]() 两点关于直线
两点关于直线![]() 对称,
对称, ![]() 为坐标原点,求
为坐标原点,求![]() 的取值范围及
的取值范围及![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某小型企业甲产品生产的投入成本![]() (单位:万元)与产品销售收入
(单位:万元)与产品销售收入![]() (单位:万元)存在较好的线性关系,下表记录了最近5次产品的相关数据.
(单位:万元)存在较好的线性关系,下表记录了最近5次产品的相关数据.
| 7 | 10 | 11 | 15 | 17 |
| 19 | 22 | 25 | 30 | 34 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)根据(1)中的回归方程,判断该企业甲产品投入成本20万元的毛利率更大还是投入成本24万元的毛利率更大(![]() )?
)?
相关公式: 
 ,
, ![]() .
.
【答案】(1)![]() .(2)投入成本20万元的毛利率更大.
.(2)投入成本20万元的毛利率更大.
【解析】试题分析:(1)由回归公式,解得线性回归方程为![]() ;(2)当
;(2)当![]() 时,
时, ![]() ,对应的毛利率为
,对应的毛利率为![]() ,当
,当![]() 时,
时, ![]() ,对应的毛利率为
,对应的毛利率为![]() ,故投入成本20万元的毛利率更大。
,故投入成本20万元的毛利率更大。
试题解析:
(1)![]() ,
, ![]() ,
,

![]() ,
, ![]() ,故
,故![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() .
.
(2)当![]() 时,
时, ![]() ,对应的毛利率为
,对应的毛利率为![]() ,
,
当![]() 时,
时, ![]() ,对应的毛利率为
,对应的毛利率为![]() ,
,
故投入成本20万元的毛利率更大.
【题型】解答题
【结束】
21
【题目】如图,在正方体![]() 中,
中, ![]() 分别是棱
分别是棱![]() 的中点,
的中点, ![]() 为棱
为棱![]() 上一点,且异面直线
上一点,且异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() .
.

(1)证明: ![]() 为
为![]() 的中点;
的中点;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆![]() 的圆心在直线
的圆心在直线![]() 上,且圆
上,且圆![]() 经过点
经过点![]() 与点
与点![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 作圆
作圆![]() 的切线,求切线所在的直线的方程.
的切线,求切线所在的直线的方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】试题分析:(1)求出线段![]() 的中点
的中点![]() ,进而得到线段
,进而得到线段![]() 的垂直平分线为
的垂直平分线为![]() ,与
,与![]() 联立得交点
联立得交点![]() ,∴
,∴![]() .则圆
.则圆![]() 的方程可求
的方程可求
(2)当切线斜率不存在时,可知切线方程为![]() .
.
当切线斜率存在时,设切线方程为![]() ,由
,由![]() 到此直线的距离为
到此直线的距离为![]() ,解得
,解得![]() ,即可到切线所在直线的方程.
,即可到切线所在直线的方程.
试题解析:((1)设 线段![]() 的中点为
的中点为![]() ,∵
,∵![]() ,
,
∴线段![]() 的垂直平分线为
的垂直平分线为![]() ,与
,与![]() 联立得交点
联立得交点![]() ,
,
∴![]() .
.
∴圆![]() 的方程为
的方程为![]() .
.
(2)当切线斜率不存在时,切线方程为![]() .
.
当切线斜率存在时,设切线方程为![]() ,即
,即![]() ,
,
则![]() 到此直线的距离为
到此直线的距离为![]() ,解得
,解得![]() ,∴切线方程为
,∴切线方程为![]() .
.
故满足条件的切线方程为![]() 或
或![]() .
.
【点睛】本题考查圆的方程的求法,圆的切线,中点弦等问题,解题的关键是利用圆的特性,利用点到直线的距离公式求解.
【题型】解答题
【结束】
20
【题目】某小型企业甲产品生产的投入成本![]() (单位:万元)与产品销售收入
(单位:万元)与产品销售收入![]() (单位:万元)存在较好的线性关系,下表记录了最近5次产品的相关数据.
(单位:万元)存在较好的线性关系,下表记录了最近5次产品的相关数据.
| 7 | 10 | 11 | 15 | 17 |
| 19 | 22 | 25 | 30 | 34 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)根据(1)中的回归方程,判断该企业甲产品投入成本20万元的毛利率更大还是投入成本24万元的毛利率更大(![]() )?
)?
相关公式: 
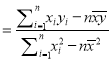 ,
, ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
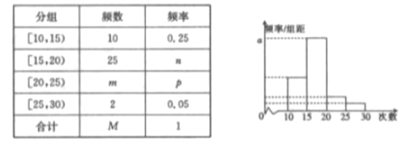
(1)求出表中![]() 及图中
及图中![]() 的值;
的值;
(2)若该校高一学生有800人,试估计该校高一学生参加社区服务的次数在区间![]() 内的人数.
内的人数.
【答案】(1)![]() ,
, ![]() ,
, ![]() ;(2)
;(2)![]() 人.
人.
【解析】试题分析:(1)由题意, ![]() 内的频数是10,频率是0.25知,
内的频数是10,频率是0.25知, ![]() ,所以
,所以![]() ,则
,则![]() ,
, ![]() .(2)高一学生有800人,分组
.(2)高一学生有800人,分组![]() 内的频率是
内的频率是![]() ,人数为
,人数为![]() 人.
人.
试题解析:
(1)由![]() 内的频数是10,频率是0.25知,
内的频数是10,频率是0.25知, ![]() ,所以
,所以![]() .
.
因为频数之和为40,所以![]() ,
, ![]() .
.
![]() .
.
因为![]() 是对应分组
是对应分组![]() 的频率与组距的商,所以
的频率与组距的商,所以![]() .
.
(2)因为该校高一学生有800人,分组![]() 内的频率是
内的频率是![]() ,
,
所以估计该校高一学生参加社区服务的次数在此区间内的人数为![]() 人.
人.
【题型】解答题
【结束】
18
【题目】已知直线![]() 经过抛物线
经过抛物线![]() 的焦点
的焦点![]() ,且与
,且与![]() 交于
交于![]() 两点.
两点.
(1)设![]() 为
为![]() 上一动点,
上一动点, ![]() 到直线
到直线![]() 的距离为
的距离为![]() ,点
,点![]() ,求
,求![]() 的最小值;
的最小值;
(2)求![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,
,![]() 。
。
Ⅰ.求函数![]() 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
Ⅱ.当![]() 时,方程
时,方程![]() 恰有两个不同的实数根,求实数
恰有两个不同的实数根,求实数![]() 的取值范围;
的取值范围;
Ⅲ.将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后所得函数
个单位后所得函数![]() 的图象关于原点中心对称,求
的图象关于原点中心对称,求![]() 的最小值。
的最小值。
查看答案和解析>>
科目: 来源: 题型:
【题目】已知定义在[﹣ ![]() ,
, ![]() ]的函数f(x)=sinx(cosx+1)﹣ax,若y=f(x)仅有一个零点,则实数a的取值范围是( )
]的函数f(x)=sinx(cosx+1)﹣ax,若y=f(x)仅有一个零点,则实数a的取值范围是( )
A.( ![]() ,2]
,2]
B.(﹣∞, ![]() )∪[2,+∞)
)∪[2,+∞)
C.[﹣ ![]() ,
, ![]() )
)
D.(﹣∞,﹣ ![]() ]∪(
]∪( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目: 来源: 题型:
【题目】为减少空气污染,某市鼓励居民用电(减少燃气或燃煤),采用分段计费的方法计算电费每月用电不超过100度仍按原标准收费,超过的部分每度按0.5元计算.
Ⅰ.设月用电x度时,应交电费y元,写出y关于x的函数关系式;
Ⅱ.小明家第一季度缴纳电费情况如下:
月份 | 一月 | 二月 | 三月 | 合计 |
缴费金额 | 76元 | 63元 | 45.6元 | 184.6元 |
问小明家第一季度共用多少度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com