
【题目】△ABC的三个内角A、B、C的对边分别是a、b、c,其面积S=a2﹣(b﹣c)2 . 若a=2,则BC边上的中线长的取值范围是 .
【答案】(1,4]
【解析】解:∵S=a2﹣(b﹣c)2=a2﹣b2﹣c2+2bc,
b2+c2﹣a2=2bccosA,
S= ![]() ,
,
∴2bc(1﹣cosA)= ![]() bcsinA,
bcsinA,
∴sinA=4﹣4cosA,
又∵sin2A+cos2A=1,
∴cosA= ![]() ,sinA=
,sinA= ![]() .
.
由正弦定理得 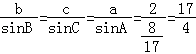 ,
,
∴b= ![]() ,c=
,c= ![]() .
.
设BC的中点为D,则CD= ![]() .
.
在△ACD中,由余弦定理得AD2=CD2+AC2﹣2ACCDcosC=1+ ![]() sin2B﹣
sin2B﹣ ![]() cosC.
cosC.
∵cosC=﹣cos(A+B)=sinAsinB﹣cosAcosB= ![]() ,
,
∴AD2=1+ ![]() sin2B﹣
sin2B﹣ ![]() (
( ![]() )=
)= ![]() sin2B+
sin2B+ ![]() sinBcosB+1=
sinBcosB+1= ![]() ×
× ![]() +
+ ![]() sin2B+1=
sin2B+1= ![]() sin2B﹣
sin2B﹣ ![]() cos2B+
cos2B+ ![]() .
.
= ![]() sin(2B﹣φ)+
sin(2B﹣φ)+ ![]() ,其中sinφ=
,其中sinφ= ![]() ,cosφ=
,cosφ= ![]() ,∴φ=
,∴φ= ![]() .
.
∴AD2= ![]() sin(2B+A﹣
sin(2B+A﹣ ![]() )+
)+ ![]() =﹣
=﹣ ![]() cos(2B+A)+
cos(2B+A)+ ![]() .
.
∵0<B<π﹣A,
∴A<2B+A<2π﹣A.
∵sinA= ![]() ,∴A
,∴A ![]() ,
,
∴当2B+A=π时,AD2取得最大值 ![]() =
= ![]() =16,
=16,
当2B+A=A或2π﹣A时,AD2取得最小值﹣ ![]() ×
× ![]() +
+ ![]() =1.
=1.
∴1<AD≤4.
所以答案是(1,4].
【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识,掌握正弦定理:![]() ,以及对余弦定理的定义的理解,了解余弦定理:
,以及对余弦定理的定义的理解,了解余弦定理:![]() ;
;![]() ;
;![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】若a和b是计算机在区间(0,2)上产生的均匀随机数,则一元二次不等式ax2+4x+4b>0(a>0)的解集不是R的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC和△ACD中,∠ACB=∠ADC=90°,∠BAC=∠CAD,⊙O是以AB为直径的圆,DC的延长线与AB的延长线交于点E.
(Ⅰ)求证:DC是⊙O的切线;
(Ⅱ)若EB=6,EC=6 ![]() ,求BC的长.
,求BC的长.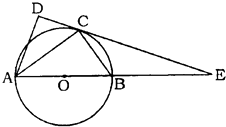
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在[﹣ ![]() ,
, ![]() ]的函数f(x)=sinx(cosx+1)﹣ax,若y=f(x)仅有一个零点,则实数a的取值范围是( )
]的函数f(x)=sinx(cosx+1)﹣ax,若y=f(x)仅有一个零点,则实数a的取值范围是( )
A.( ![]() ,2]
,2]
B.(﹣∞, ![]() )∪[2,+∞)
)∪[2,+∞)
C.[﹣ ![]() ,
, ![]() )
)
D.(﹣∞,﹣ ![]() ]∪(
]∪( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆N的标准方程为(x-5)2+(y-6)2=a2(a>0).
(1)若点M(6,9)在圆上,求a的值;
(2)已知点P(3,3)和点Q(5,3),线段PQ(不含端点)与圆N有且只有一个公共点,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A={x|2x2+ax+2=0},B={x|x2+3x+2a=0},A∩B={2}.
(1)求a的值及集合A、B;
(2)设集合U=A∪B,求(CuA)∪(CuB)的所有子集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,且anan+1=2n , n∈N* , 则数列{an}的通项公式为( )
A.an=( ![]() )n﹣1
)n﹣1
B.an=( ![]() )n
)n
C.an= ![]()
D.an= ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com