
科目: 来源: 题型:
【题目】已知点A(0,﹣2),椭圆E: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,F是椭圆的焦点,直线AF的斜率为
,F是椭圆的焦点,直线AF的斜率为 ![]() ,O为坐标原点.
,O为坐标原点.
(Ⅰ)求E的方程;
(Ⅱ)设过点A的直线l与E相交于P,Q两点,当△OPQ的面积最大时,求l的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一个角形海湾AOB,∠AOB=2θ(常数θ为锐角).拟用长度为l(l为常数)的围网围成一个养殖区,有以下两种方案可供选择:
方案一 如图1,围成扇形养殖区OPQ,其中 ![]() =l;
=l;
方案二 如图2,围成三角形养殖区OCD,其中CD=l;
(1)求方案一中养殖区的面积S1;
(2)求证:方案二中养殖区的最大面积S2= ![]() ;
;
(3)为使养殖区的面积最大,应选择何种方案?并说明理由
查看答案和解析>>
科目: 来源: 题型:
【题目】潮州统计局就某地居民的月收入调查了![]() 人,并根据所得数据画了样本的频率分
人,并根据所得数据画了样本的频率分
布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在![]() )。
)。

(1)求居民月收入在![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这![]() 人中分层抽样方法抽出
人中分层抽样方法抽出![]() 人作进一步分析,则月收入在
人作进一步分析,则月收入在![]() 的这段应抽多少人?
的这段应抽多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】某校按分层抽样的方法从高中三个年级抽取部分学生调查,从三个年级抽取人数的比例为如图所示的扇形面积比,已知高二年级共有学生1 200人,并从中抽取了40人.

(1)该校的总人数为多少?(2)三个年级分别抽取多少人?
(3)在各层抽样中可采取哪种抽样方法?
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂生产的产品![]() 的直径均位于区间
的直径均位于区间![]() 内(单位:
内(单位: ![]() ).若生产一件产品
).若生产一件产品![]() 的直径位于区间
的直径位于区间![]() 内该厂可获利分别为10,30,20,10(单位:元),现从该厂生产的产品
内该厂可获利分别为10,30,20,10(单位:元),现从该厂生产的产品![]() 中随机抽取200件测量它们的直径,得到如图所示的频率分布直方图.
中随机抽取200件测量它们的直径,得到如图所示的频率分布直方图.
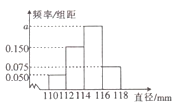
(1)求![]() 的值,并估计该厂生产一件
的值,并估计该厂生产一件![]() 产品的平均利润;
产品的平均利润;
(2)现用分层抽样法从直径位于区间![]() 内的产品中随机抽取一个容量为5的样本,从样本中随机抽取两件产品进行检测,求两件产品中至多有一件产品的直径位于区间
内的产品中随机抽取一个容量为5的样本,从样本中随机抽取两件产品进行检测,求两件产品中至多有一件产品的直径位于区间![]() 内的槪率.
内的槪率.
查看答案和解析>>
科目: 来源: 题型:
【题目】有一个公益广告说:“若不注意节约用水,那么若干年后,最有一滴水只能是我们的眼泪。”我国是水资源匮乏的国家。为鼓励节约用水,某市打算出台一项水费政策措施,规定:每一季度每人用水量不超过5吨时,每吨水费收基本价1.3元;若超过5吨而不超过6吨时,超过部分的水费加收200%;若超过6吨而不超过7吨时,超过部分的水费加收400%。设某人本季度实际用水量为![]() 吨,应交水费为f(x),(1)求
吨,应交水费为f(x),(1)求![]() 的值;(2)试求出函数f(x)的解析式。
的值;(2)试求出函数f(x)的解析式。
查看答案和解析>>
科目: 来源: 题型:
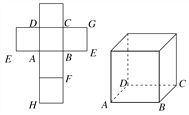
【题目】一个正方体的平面展开图及该正方体的直观图的示意图如图所示.
(1)请按字母F、G、H标记在正方体相应地顶点处(不需要说明理由);
(2)判断平面BEG与平面ACH的位置关系.并说明你的结论;
(3)证明:直线DF⊥平面BEG.
查看答案和解析>>
科目: 来源: 题型:
【题目】某技术公司新开发了A,B两种新产品,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品,现随机抽取这两种产品各100件进行检测,检测结果统计如下:
测试指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
产品A | 8 | 12 | 40 | 32 | 8 |
产品B | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计产品A,产品B为正品的概率;
(2)生产一件产品A,若是正品可盈利80元,次品则亏损10元;生产一件产品B,若是正品可盈利100元,次品则亏损20元;在(1)的前提下.记X为生产一件产品A和一件产品B所得的总利润,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,椭圆![]() 的左、右焦点为
的左、右焦点为![]() ,
, ![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() ,若
,若![]() ,
, ![]() 与
与![]() 轴垂直,且
轴垂直,且![]() .
.
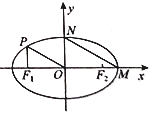
(1)求椭圆的方程;
(2)过点![]() 且不垂直与坐标轴的直线与椭圆交于
且不垂直与坐标轴的直线与椭圆交于![]() ,
, ![]() 两点,已知点
两点,已知点![]() ,当
,当![]() 时,求满足
时,求满足![]() 的直线
的直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com