
科目: 来源: 题型:
【题目】[2019·朝鲜中学]在如图所示的程序框图中,有这样一个执行框![]() ,其中的函数关系式为
,其中的函数关系式为![]() ,程序框图中的
,程序框图中的![]() 为函数
为函数![]() 的定义域.
的定义域.
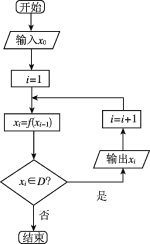
(1)若输入![]() ,请写出输出的所有
,请写出输出的所有![]() 的值;
的值;
(2)若输出的所有![]() 都相等,试求输入的初始值
都相等,试求输入的初始值![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】学校艺术节对同一类的![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
, ![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学只有两位说的话是对的,则获得一等奖的作品是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生在规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是
A. 甲地:总体均值为3,中位数为4 B. 乙地:总体均值为1,总体方差大于0
C. 丙地:中位数为2,众数为3 D. 丁地:总体均值为2,总体方差为3
查看答案和解析>>
科目: 来源: 题型:
【题目】现从某医院中随机抽取了7位医护人员的关爱患者考核分数(患者考核:10分制),用相关的特征量![]() 表示;医护专业知识考核分数(试卷考试:100分制),用相关的特征量
表示;医护专业知识考核分数(试卷考试:100分制),用相关的特征量![]() 表示,数据如下表:
表示,数据如下表:
特征量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 98 | 88 | 96 | 91 | 90 | 92 | 96 |
| 9.9 | 8.6 | 9.5 | 9.0 | 9.1 | 9.2 | 9.8 |
(1)求![]() 关于
关于![]() 的线性回归方程(计算结果精确到0.01);
的线性回归方程(计算结果精确到0.01);
(2)利用(1)中的线性回归方程,分析医护专业考核分数的变化对关爱患者考核分数的影响,并估计某医护人员的医护专业知识考核分数为95分时,他的关爱患者考核分数(精确到0.1)
附:回归直线方程![]() 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为
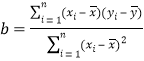 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】A市某机构为了调查该市市民对我国申办2034年足球世界杯的态度,随机选取了140位市民进行调查,调查结果统计如下:
支持 | 不支持 | 总计 | |
男性市民 | 60 | ||
女性市民 | 50 | ||
合计 | 70 | 140 |
(I)根据已知数据,把表格数据填写完整;
(II)利用(1)完成的表格数据回答下列问题:
(ⅰ)能否在犯错误的概率不超过0.001的前提下认为性别与支持申办足球世界杯有关;
(ⅱ)已知在被调查的支持申办足球世界杯的男性市民中有5位退休老人,其中2位是教师,现从这5位退休老人中随机抽取3人,求至多有1位老师的概率。
附:![]() ,其中
,其中![]()
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数g(x)=ax2﹣2ax+1+b(a>0).
(1)在区间[2,3]上的最大值为4,最小值为1,求实数a,b的值;
(2)若b=1,对任意x∈[1,2),g(x)≥0恒成立,则a的范围;
(3)若b=1,对任意a∈[2,3],g(x)≥0恒成立,则x的范围;
(4)在(1)的条件下记f(x)=g(|x|),若不等式f(log2k)>f(2)成立,求实数k的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f1(x)=![]() x2,f2(x)=alnx(其中a>0).
x2,f2(x)=alnx(其中a>0).
(1)求函数f(x)=f1(x)·f2(x)的极值;
(2)若函数g(x)=f1(x)-f2(x)+(a-1)x在区间(![]() ,e)内有两个零点,求正实数a的取值范围;
,e)内有两个零点,求正实数a的取值范围;
(3)求证:当x>0时,![]() .(说明:e是自然对数的底数,e=2.71828…)
.(说明:e是自然对数的底数,e=2.71828…)
查看答案和解析>>
科目: 来源: 题型:
【题目】设集合P={x|x2﹣x﹣6<0},Q={2a≤x≤a+3}.
(1)若P∪Q=P,求实数a的取值范围;
(2)若P∩Q=,求实数a的取值范围;
(3)若P∩Q={x|0≤x<3},求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=ax2-(a+2)x+lnx
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若对任意x1,x2∈(0,+∞),x1<x2,有f(x1)+2x1<f(x2)+2x2恒成立,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com