
科目: 来源: 题型:
【题目】某校有![]() ,
,![]() ,
,![]() ,
,![]() 四件作品参加航模类作品比赛.已知这四件作品中恰有两件获奖.在结果揭晓前,甲、乙、丙、丁四位同学对这四件参赛作品的获奖情况预测如下:
四件作品参加航模类作品比赛.已知这四件作品中恰有两件获奖.在结果揭晓前,甲、乙、丙、丁四位同学对这四件参赛作品的获奖情况预测如下:
甲说:“![]() 、
、![]() 同时获奖”;
同时获奖”;
乙说:“![]() 、
、![]() 不可能同时获奖”;
不可能同时获奖”;
丙说:“![]() 获奖”;
获奖”;
丁说:“![]() 、
、![]() 至少一件获奖”.
至少一件获奖”.
如果以上四位同学中有且只有二位同学的预测是正确的,则获奖的作品是( )
A. 作品![]() 与作品
与作品![]() B. 作品
B. 作品![]() 与作品
与作品![]() C. 作品
C. 作品![]() 与作品
与作品![]() D. 作品
D. 作品![]() 与作品
与作品![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司计划购买2台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:

以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率,记![]() 表示2台机器三年内共需更换的易损零件数,
表示2台机器三年内共需更换的易损零件数,![]() 表示购买2台机器的同时购买的易损零件数.
表示购买2台机器的同时购买的易损零件数.
(Ⅰ)求![]() 的分布列;
的分布列;
(Ⅱ)若要求![]() ,确定
,确定![]() 的最小值;
的最小值;
(Ⅲ)以购买易损零件所需费用的期望值为决策依据,在![]() 与
与![]() 之中选其一,应选用哪个?
之中选其一,应选用哪个?
查看答案和解析>>
科目: 来源: 题型:
【题目】在一次抽样调查中测得样本的5个样本点,数值如下表:
| 0.25 | 0.5 | 1 | 2 | 4 |
| 16 | 12 | 5 | 2 | 1 |
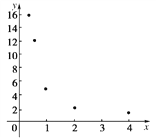
(1)根据散点图判断,![]() 哪一个适宜作为
哪一个适宜作为![]() 关于
关于![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果试建立![]() 与
与![]() 之间的回归方程.(注意
之间的回归方程.(注意![]() 或
或![]() 计算结果保留整数)
计算结果保留整数)
(3)由(2)中所得设z=![]() +
+![]() 且
且![]() ,试求z的最小值。
,试求z的最小值。
参考数据及公式如下:
![]() ,
,![]() ,
,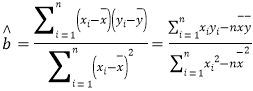
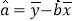
查看答案和解析>>
科目: 来源: 题型:
【题目】某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生的样本数据?
(2)根据这300样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据的分组区间为: ![]() .估计该校学生每周平均体育运动时间超过4小时的概率;
.估计该校学生每周平均体育运动时间超过4小时的概率;

(3)在样本数据中,有60位女生的每周平均体育运动时间超过4小时,请完成每周平均体育运动时间与性别的列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
附: 
查看答案和解析>>
科目: 来源: 题型:
【题目】要得到函数![]() 的图象, 只需将函数
的图象, 只需将函数![]() 的图象( )
的图象( )
A. 所有点的横坐标伸长到原来的2倍(纵坐标不变), 再将所得的图像向左平移![]() 个单位.
个单位.
B. 所有点的横坐标伸长到原来的2倍(纵坐标不变), 再将所得的图像向左平移![]() 个单位.
个单位.
C. 所有点的横坐标缩短到原来的![]() 倍(纵坐标不变), 再将所得的图像向左平移
倍(纵坐标不变), 再将所得的图像向左平移![]() 个单位.
个单位.
D. 所有点的横坐标缩短到原来的![]() 倍(纵坐标不变), 再将所得的图像向左平移
倍(纵坐标不变), 再将所得的图像向左平移![]() 个单位.
个单位.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用,现有6名男志愿者![]() 和4名女志愿者
和4名女志愿者![]() ,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示。
,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示。
(1)求接受甲种心理暗示的志愿者中包含![]() 但不包含
但不包含![]() 的概率;
的概率;
(2)用X表示接受乙种心理暗示的女志愿者人数,求X的分布列与数学期望E(X).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com