
科目: 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,与双曲线x2﹣y2=1的渐近线有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C的方程为( )
,与双曲线x2﹣y2=1的渐近线有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C的方程为( )
A.![]() +
+ ![]() =1
=1
B.![]() +
+ ![]() =1
=1
C.![]() +
+ ![]() =1
=1
D.![]() +
+ ![]() =1
=1
查看答案和解析>>
科目: 来源: 题型:
【题目】已知x>0,由不等式x+ ![]() ≥2
≥2 ![]() =2,x+
=2,x+ ![]() =
= ![]() ≥3
≥3 ![]() =3,…,可以推出结论:x+
=3,…,可以推出结论:x+ ![]() ≥n+1(n∈N*),则a=( )
≥n+1(n∈N*),则a=( )
A.2n
B.3n
C.n2
D.nn
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)= ![]() sin2x+
sin2x+ ![]() sin2x.
sin2x.
(1)求函数f(x)的单调递减区间;
(2)在△ABC中,角A,B,C的对边分别为a,b,c,若f( ![]() )=
)= ![]() ,△ABC的面积为3
,△ABC的面积为3 ![]() ,求a的最小值.
,求a的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=sin(2x+ ![]() )(x∈R),下面结论错误的是( )
)(x∈R),下面结论错误的是( )
A.函数f(x)的最小正周期为π
B.函数f(x)是偶函数
C.函数f(x)的图象关于直线 ![]() 对称
对称
D.函数f(x)在区间[0, ![]() ]上是增函数
]上是增函数
查看答案和解析>>
科目: 来源: 题型:
【题目】我校高二年级共2000名学生,其中男生1200人.为调查学生们的手机使用情况,采用分层抽样的方法,随机抽取100位学生每周平均使用手机上网时间的样本数据(单位:小时).根据这100个数据,得到学生每周平均使用手机上网时间的频率分布直方图(如图所示),其中样本数据分组区间分别为![]() .
.
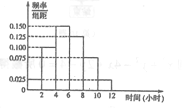
(1)应收集男生、女生样本数据各多少人?
(2)估计我校高二年级学生每周平均使用手机上网时间超过4小时的概率.
(3)将平均每周使用手机上网时间在![]() 内定义为“长时间使用手机”,在
内定义为“长时间使用手机”,在![]() 内定义为“短时间使用手机”.在样本数据中,有25名学生不近视.请完成下列2×2列联表,并判断是否有99.5%的把握认为“学生每周使用手机上网时间与近视程度有关”.
内定义为“短时间使用手机”.在样本数据中,有25名学生不近视.请完成下列2×2列联表,并判断是否有99.5%的把握认为“学生每周使用手机上网时间与近视程度有关”.
近视 | 不近视 | 合计 | |
长时间使用手机上网 | |||
短时间使用手机上网 | 15 | ||
合计 | 25 |
附:![]()
| 0.100 | 0.050 | 0.010 | 0.005 |
| 2.706 | 6.635 | 7.879 |
查看答案和解析>>
科目: 来源: 题型:
【题目】为比较甲、乙两地某月14时的气温状况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图.考虑以下结论:
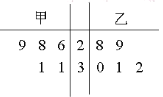
①甲地该月14时的平均气温低于乙地该月14时的平均气温;
②甲地该月14时的平均气温高于乙地该月14时的平均气温;
③甲地该月14时的平均气温的标准差小于乙地该月14时的气温的标准差;
④甲地该月14时的平均气温的标准差大于乙地该月14时的气温的标准差.
其中根据茎叶图能得到的统计结论的标号为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆![]() :
:![]() ,直线
,直线![]() :
:![]() .
.
(1)若直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,求实数
,求实数![]() 的值;
的值;
(2)当![]() 时,由直线
时,由直线![]() 上的动点
上的动点![]() 引圆
引圆![]() 的两条切线,若切点分别为
的两条切线,若切点分别为![]() ,
,![]() ,则在直线
,则在直线![]() 上是否存在一个定点?若存在,求出该定点的坐标;若不存在,请说明理由.
上是否存在一个定点?若存在,求出该定点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某班级共派出![]() 个男生和
个男生和![]() 个女生参加学校运动会的入场仪式,其中男生倪某为领队.入场时,领队男生倪某必须排第一个,然后女生整体在男生的前面,排成一路纵队入场,共有
个女生参加学校运动会的入场仪式,其中男生倪某为领队.入场时,领队男生倪某必须排第一个,然后女生整体在男生的前面,排成一路纵队入场,共有![]() 种排法;入场后,又需从男生(含男生倪某)和女生中各选一名代表到主席台服务,共有
种排法;入场后,又需从男生(含男生倪某)和女生中各选一名代表到主席台服务,共有![]() 种选法.(1)试求
种选法.(1)试求![]() 和
和![]() ; (2)判断
; (2)判断![]() 和
和![]() 的大小(
的大小(![]() ),并用数学归纳法证明.
),并用数学归纳法证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】函数f(x)=sin(2x+φ)(|φ|<π)的图象向左平移 ![]() 个单位后关于原点对称,则函数f(x)在[0,
个单位后关于原点对称,则函数f(x)在[0, ![]() ]上的最小值为( )
]上的最小值为( )
A.﹣ ![]()
B.﹣ ![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com