
科目: 来源: 题型:
【题目】德国数学家科拉茨1937年提出了一个著名的猜想:任给一个正整数n,如果n是偶数,就将它减半(即![]() );如果n是奇数,则将它乘3加1(即3n+1),不断重复这样的运算,经过有限步后,一定可以得到1. 对于科拉茨猜想,目前谁也不能证明,也不能否定,现在请你研究:如果对正整数n(首项)按照上述规则施行变换后的第8项为1(注:l可以多次出现),则n的所有不同值的个数为
);如果n是奇数,则将它乘3加1(即3n+1),不断重复这样的运算,经过有限步后,一定可以得到1. 对于科拉茨猜想,目前谁也不能证明,也不能否定,现在请你研究:如果对正整数n(首项)按照上述规则施行变换后的第8项为1(注:l可以多次出现),则n的所有不同值的个数为
A. 4 B. 6 C. 8 D. 32
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,四棱锥P﹣ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点.
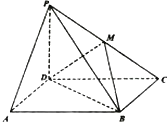
(1)求证:AP∥平面MBD;
(2)若AD⊥PB,求证:BD⊥平面PAD.
查看答案和解析>>
科目: 来源: 题型:
【题目】以平面直角坐标系![]() 的原点为极点,
的原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位.若直线
轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位.若直线![]() 的参数方程为
的参数方程为![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(I)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(II)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,若
两点,若![]() 点的直角坐标为
点的直角坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着人们生活水平的不断提高,家庭理财越来越引起人们的重视.某一调查机构随机调查了5个家庭的月收入与月理财支出(单位:元)的情况,如下表所示:
月收入 | 8 | 10 | 9 | 7 | 11 |
月理财支出 |
|
|
|
|
|
(I)在下面的坐标系中画出这5组数据的散点图;

(II)根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(III)根据(II)的结果,预测当一个家庭的月收入为![]() 元时,月理财支出大约是多少元?
元时,月理财支出大约是多少元?
(附:回归直线方程![]() 中,
中, ,
,![]() .)
.)
查看答案和解析>>
科目: 来源: 题型:
【题目】己知抛物线y=x2+m的顶点M到直线l:![]() (t为参数)的距离为1
(t为参数)的距离为1
(Ⅰ)求m:
(Ⅱ)若直线l与抛物线相交于A,B两点,与y轴交于N点,求|S△MAN﹣S△MBN|的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】洛萨·科拉茨是德国数学家,他在1937年提出了一个著名的猜想:任给一个正整数![]() ,如果
,如果![]() 是偶数,就将它减半(即
是偶数,就将它减半(即![]() );如果
);如果![]() 是奇数,则将它乘3加1(即
是奇数,则将它乘3加1(即![]() ),不断重复这样的运算,经过有限步后,一定可以得到1,如初始正整数为6,按照上述变换规则,我们得到一个数列:6,3,10,5,16,8,4,2,1.对科拉茨猜想,目前谁也不能证明,更不能否定,如果对正整数
),不断重复这样的运算,经过有限步后,一定可以得到1,如初始正整数为6,按照上述变换规则,我们得到一个数列:6,3,10,5,16,8,4,2,1.对科拉茨猜想,目前谁也不能证明,更不能否定,如果对正整数![]() 按照上述规则实施变换(注:1可以多次出现)后的第九项为1,则
按照上述规则实施变换(注:1可以多次出现)后的第九项为1,则![]() 的所有可能取值的集合为_________.
的所有可能取值的集合为_________.
查看答案和解析>>
科目: 来源: 题型:
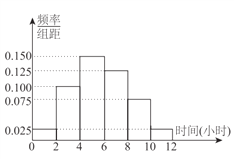
【题目】某中学共有5000人,其中男生3500人,女生1500人,为了了解该校学生每周平均体育锻炼时间的情况以及该校学生每周平均体育锻炼时间是否与性别有关,现在用分层抽样的方法从中收集300位学生每周平均体育锻炼时间的样本数据(单位:小时),其频率分布直方图如下:
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
已知在样本数据中,有60位女生的每周平均体育锻炼时间超过4小时,根据独立性检验原理,我们( )
A. 没有理由认为“该校学生每周平均体育锻炼时间与性别有关”
B. 有![]() 的把握认为“该校学生每周平均体育锻炼时间与性别有关”
的把握认为“该校学生每周平均体育锻炼时间与性别有关”
C. 有![]() 的把握认为“该校学生每周平均体育锻炼时间与性别无关”
的把握认为“该校学生每周平均体育锻炼时间与性别无关”
D. 有![]() 的把握认为“该校学生每周平均体育锻炼时间与性别有关”
的把握认为“该校学生每周平均体育锻炼时间与性别有关”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com