【题目】已知a∈R，函数f（x）=x3﹣3x2+3ax﹣3a+3．
（1）求曲线y=f（x）在点（1，f（1））处的切线方程；
（2）当x∈[0，2]时，求|f（x）|的最大值．

【题目】如图所示，在平面上，点，点在单位圆上且 .

（1）若点，求的值：

（2）若，四边形的面积用表示，求的取值范围.

【题目】如图，点P（0，﹣1）是椭圆C1： + =1（a＞b＞0）的一个顶点，C1的长轴是圆C2：x2+y2=4的直径，l1 ， l2是过点P且互相垂直的两条直线，其中l1交圆C2于A、B两点，l2交椭圆C1于另一点D．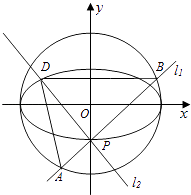

（1）求椭圆C1的方程；
（2）求△ABD面积的最大值时直线l1的方程．

【题目】如图，在四面体A﹣BCD中，AD⊥平面BCD，BC⊥CD，AD=2，BD=2 ．M是AD的中点，P是BM的中点，点Q在线段AC上，且AQ=3QC．

（1）证明：PQ∥平面BCD；
（2）若二面角C﹣BM﹣D的大小为60°，求∠BDC的大小．

【题目】如图四边形ABCD为菱形，G为AC与BD交点，，

（I）证明：平面平面；

（II）若， 三棱锥的体积为，求该三棱锥的侧面积.

【题目】一半径为的水轮如图所示，水轮圆心距离水面；已知水轮按逆时针做匀速转动，每转一圈，如果当水轮上点从水中浮现时（图中点）开始计算时间.

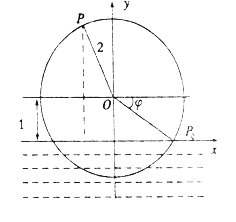
（1）以水轮所在平面与水面的交线为轴，以过点且与水面垂直的直线为轴，建立如图所示的直角坐标系，将点距离水面的高度表示为时间的函数；

（2）点第一次到达最高点大约要多长时间？

【题目】设袋子中装有a个红球，b个黄球，c个蓝球，且规定：取出一个红球得1分，取出一个黄球2分，取出蓝球得3分．
（1）当a=3，b=2，c=1时，从该袋子中任取（有放回，且每球取到的机会均等）2个球，记随机变量ξ为取出此2球所得分数之和．求ξ分布列；
（2）从该袋子中任取（且每球取到的机会均等）1个球，记随机变量η为取出此球所得分数．若 ，求a：b：c．

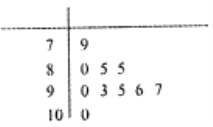
（1）计算这10名学生的成绩的均值和方差；

（2）给出正态分布的数据：P（μ﹣σ＜X＜μ+σ）=0.6826，P（μ﹣2σ＜X＜μ+2σ）=0.9544．

由（1）估计从全市随机抽取一名学生的成绩在（76，97）的概率．

(I)从乙班随机抽取2名学生的成绩,记“成绩优秀”的个数为，求的分布列和数学期望；

(II)根据频率分布直方图填写下面2 x2列联表,并判断是否有95％的把握认为:“成绩优秀”与教学方式有关.

附：

【题目】（本小题满分16分）已知是虚数， 是实数．

（1）求为何值时， 有最小值，并求出|的最小值；

（2）设，求证： 为纯虚数．