【题目】北京某附属中学为了改善学生的住宿条件，决定在学校附近修建学生宿舍，学校总务办公室用1000万元从政府购得一块廉价土地，该土地可以建造每层1000平方米的楼房，楼房的每平方米建筑费用与建筑高度有关，楼房每升高一层，整层楼每平方米建筑费用提高0.02万元，已知建筑第5层楼房时，每平方米建筑费用为0.8万元．

（1）若学生宿舍建筑为层楼时，该楼房综合费用为万元，综合费用是建筑费用与购地费用之和），写出的表达式；

（2）为了使该楼房每平方米的平均综合费用最低，学校应把楼层建成几层？此时平均综合费用为每平方米多少万元？

【答案】（1）；（2）学校应把楼层建成层，此时平均综合费用为每平方米万元

【解析】

由已知求出第层楼房每平方米建筑费用为万元，得到第层楼房建筑费用，由楼房每升高一层，整层楼建筑费用提高万元，然后利用等差数列前项和求建筑层楼时的综合费用；

设楼房每平方米的平均综合费用为，则，然后利用基本不等式求最值．

解：由建筑第5层楼房时，每平方米建筑费用为万元，

且楼房每升高一层，整层楼每平方米建筑费用提高万元，

可得建筑第1层楼房每平方米建筑费用为：万元．

建筑第1层楼房建筑费用为：万元．

楼房每升高一层，整层楼建筑费用提高：万元．

建筑第x层楼时，该楼房综合费用为：．

；

设该楼房每平方米的平均综合费用为，

则：，

当且仅当，即时，上式等号成立．

学校应把楼层建成10层，此时平均综合费用为每平方米万元．

【点睛】

本题考查简单的数学建模思想方法，训练了等差数列前n项和的求法，训练了利用基本不等式求最值，是中档题．

【题型】解答题
【结束】
20

【题目】已知．

（1）求函数的最小正周期和对称轴方程；

（2）若，求的值域．

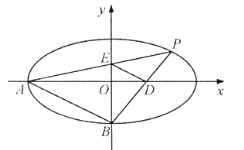
【题目】如图，在平面直角坐标系中，椭圆：的离心率为，焦点到相应准线的距离为，，分别为椭圆的左顶点和下顶点，为椭圆上位于第一象限内的一点，交轴于点，交轴于点.

（1）求椭圆的标准方程；

（2）若，求的值；

（3）求证：四边形的面积为定值.

【题目】已知集合M={（x，y）|y=f（x）}，若对于任意实数对（x1 ， y1）∈M，存在（x2 ， y2）∈M，使x1x2+y1y2=0成立，则称集合M具有∟性，给出下列四个集合： ①M={（x，y）|y=x3﹣2x2+3}； ②M={（x，y）|y=log2（2﹣x）}；
③M={（x，y）|y=2﹣2x}； ④M={（x，y）|y=1﹣sinx}；
其中具有∟性的集合的个数是（ ）
A.1
B.2
C.3
D.4

【题目】如图，正方体的棱长为1，为中点，连接，则异面直线和所成角的余弦值为_____．

【答案】

【解析】

连接CD1，CM，由四边形A1BCD1为平行四边形得A1B∥CD1，即∠CD1M为异面直线A1B和D1M所成角，再由已知求△CD1M的三边长，由余弦定理求解即可．

如图，

连接，由，可得四边形为平行四边形，

则，∴为异面直线和所成角，

由正方体的棱长为1，为中点，

得，．

在中，由余弦定理可得，．

∴异面直线和所成角的余弦值为．

故答案为：．

【点睛】

本题考查异面直线所成角的求法，异面直线所成的角常用方法有：将异面直线平移到同一平面中去，达到立体几何平面化的目的；或者建立坐标系，通过求直线的方向向量得到直线夹角或其补角.

【题型】填空题
【结束】
16

【题目】在中，角所对的边分别是，是的中点，，，面积的最大值为_____．

【题目】已知，则_____．

【答案】

【解析】

分子分母同时除以，把目标式转为的表达式，代入可求.

，则

故答案为：．

【点睛】

本题考查三角函数的化简求值，常用方法：(1)弦切互化法:主要利用公式, 形如等类型可进行弦化切；（2）“1”的灵活代换和的关系进行变形、转化.

【题型】填空题
【结束】
15

【题目】如图，正方体的棱长为1，为中点，连接，则异面直线和所成角的余弦值为_____．

【题目】已知点A（1，2），过点P（5，﹣2）的直线与抛物线y2=4x相交于B，C两点，则△ABC是（ ）
A.直角三角形
B.钝角三角形
C.锐角三角形
D.不能确定

【题目】交通管理部门为了解机动车驾驶员（简称驾驶员）对某新法规的知晓情况，对甲、乙、丙、丁四个社区做分层抽样调查．假设四个社区驾驶员的总人数为N，其中甲社区有驾驶员96人．若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为12，21，25，43，则这四个社区驾驶员的总人数N为（ ）
A.101
B.808
C.1212
D.2012

【题目】在△ABC中，角A，B，C所对的分别为a，b，c，且acosB=（3c﹣b）cosA．
（1）若asinB=2 ，求b；
（2）若a=2 ，且△ABC的面积为 ，求△ABC的周长．

（1）求q2的值；
（2）求随机变量ξ的数学期望Eξ；
（3）试比较该同学选择在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小．

【题目】如图，在四棱锥P﹣ABCD中，PD⊥底面ABCD，底面ABCD是直角梯形，AB∥DC，AB⊥AD，AB=3，CD=2，PD=AD=5．
（1）在PD上确定一点E，使得PB∥平面ACE，并求 的值；
（2）在（1）条件下，求平面PAB与平面ACE所成锐二面角的余弦值．