
科目: 来源: 题型:
【题目】已知曲线C: ![]() =1(y≥0),直线l:y=kx+1与曲线C交于A,D两点,A,D两点在x轴上的射影分别为点B,C.记△OAD的面积S1 , 四边形ABCD的面积为S2 . (Ⅰ)当点B坐标为(﹣1,0)时,求k的值;
=1(y≥0),直线l:y=kx+1与曲线C交于A,D两点,A,D两点在x轴上的射影分别为点B,C.记△OAD的面积S1 , 四边形ABCD的面积为S2 . (Ⅰ)当点B坐标为(﹣1,0)时,求k的值;
(Ⅱ)若S1= ![]() ,求线段AD的长;
,求线段AD的长;
(Ⅲ)求 ![]() 的范围.
的范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】德国数学家科拉茨1937年提出了一个著名的猜想:任给一个正整数n,如果n是偶数,就将它减半(即![]() );如果n是奇数,则将它乘3加1(即3n+1),不断重复这样的运算,经过有限步后,一定可以得到1. 对于科拉茨猜想,目前谁也不能证明,也不能否定,现在请你研究:如果对正整数n(首项)按照上述规则施行变换后的第8项为1(注:l可以多次出现),则n的所有不同值的个数为
);如果n是奇数,则将它乘3加1(即3n+1),不断重复这样的运算,经过有限步后,一定可以得到1. 对于科拉茨猜想,目前谁也不能证明,也不能否定,现在请你研究:如果对正整数n(首项)按照上述规则施行变换后的第8项为1(注:l可以多次出现),则n的所有不同值的个数为
A. 4 B. 6 C. 8 D. 32
查看答案和解析>>
科目: 来源: 题型:
【题目】某险种的基本保费为![]() (单位:元),继续购买该险种的投保人称为续保人,续保人的本年度的保费与其上年度的出险次数的关联如下:
(单位:元),继续购买该险种的投保人称为续保人,续保人的本年度的保费与其上年度的出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 |
|
保费 |
|
|
|
|
|
|
设该险种一续保人一年内出险次数与相应概率如下:
一年内出险次数 | 0 | 1 | 2 | 3 | 4 |
|
概率 | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0.05 |
(Ⅰ)求一续保人本年度的保费高于基本保费的概率;
(Ⅱ)若一续保人本年度的保费高于基本保费,求其保费比基本保费高出![]() 的概率;
的概率;
(Ⅲ)求续保人本年度的平均保费与基本保费的比值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=ex(x2+ax+a). (I)当a=1时,求函数f(x)的单调区间;
(Ⅱ)若关于x的不等式f(x)≤ea在[a,+∞)上有解,求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知四棱锥P﹣ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PB=PD=2,PA= ![]() .
. 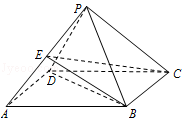
(Ⅰ)求证:BD⊥PC;
(Ⅱ)若E是PA的中点,求三棱锥P﹣BCE的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=x2+ ![]() ,现有一组数据,绘制得到茎叶图,且茎叶图中的数据的平均数为2.(茎叶图中的数据均为小数,其中茎为整数部分,叶为小数部分)
,现有一组数据,绘制得到茎叶图,且茎叶图中的数据的平均数为2.(茎叶图中的数据均为小数,其中茎为整数部分,叶为小数部分) 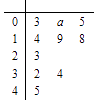
(Ⅰ)求a的值;
(Ⅱ)现从茎叶图小于3的数据中任取2个数据分别替换m的值,求恰有1个数据使得函数f(x)没有零点的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,圆形纸片的圆心为![]() ,半径为1,该纸片上的等边三角形
,半径为1,该纸片上的等边三角形![]() 的中心为
的中心为![]() .
.![]() 、
、![]() 、
、![]() 为圆
为圆![]() 上的点,
上的点,![]() ,
,![]() ,
,![]() 分别是以
分别是以![]() ,
,![]() ,
,![]() 为底边的等腰三角形.沿虚线剪开后,分别以
为底边的等腰三角形.沿虚线剪开后,分别以![]() ,
,![]() ,
,![]() 为折痕折起
为折痕折起![]() ,
,![]() ,
,![]() ,使得
,使得![]() 、
、![]() 、
、![]() 重合,得到三棱锥.当
重合,得到三棱锥.当![]() 的边长变化时,所得三棱锥体积的最大值为__________.
的边长变化时,所得三棱锥体积的最大值为__________.

查看答案和解析>>
科目: 来源: 题型:
【题目】定义“规范01数列”![]() 如下:
如下:![]() 共有
共有![]() 项,其中
项,其中![]() 项为0,
项为0,![]() 项为1,且对任意
项为1,且对任意![]() ,
,![]() ,
,![]() ,…,
,…,![]() 中0的个数不少于1的个数.若
中0的个数不少于1的个数.若![]() ,则不同的“规范01数列”共有( )
,则不同的“规范01数列”共有( )
A. 14个 B. 13个 C. 15个 D. 12个
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() 的图像是由函数
的图像是由函数![]() 的图像经如下变换得到:先将
的图像经如下变换得到:先将![]() 图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移
图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移![]() 个单位长度.
个单位长度.
(Ⅰ)求函数![]() 的解析式,并求其图像的对称轴方程;
的解析式,并求其图像的对称轴方程;
(Ⅱ)已知关于![]() 的方程
的方程![]() 在
在![]() 内有两个不同的解
内有两个不同的解![]() .
.
(1)求实数m的取值范围;
(2)证明:![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知等比数列![]() 的前
的前![]() 项和为
项和为![]() ,公比
,公比![]() ,
,![]() ,
,![]() .
.
(1)求等比数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求
,求![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)将已知两式作差,利用等比数列的通项公式,可得公比,由等比数列的求和可得首项,进而得到所求通项公式;(2)求得bn=n,![]() ,由裂项相消求和可得答案.
,由裂项相消求和可得答案.
(1)等比数列![]() 的前
的前![]() 项和为
项和为![]() ,公比
,公比![]() ,
,![]() ①,
①,
![]() ②.
②.
②﹣①,得![]() ,则
,则![]() ,
,
又![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以![]() ;
;
(2)![]() ,
,![]()
所以前![]() 项和
项和![]() .
.
【点睛】
裂项相消法适用于形如 (其中
(其中![]() 是各项均不为零的等差数列,c为常数)的数列. 裂项相消法求和,常见的有相邻两项的裂项求和,还有一类隔一项的裂项求和,如
是各项均不为零的等差数列,c为常数)的数列. 裂项相消法求和,常见的有相邻两项的裂项求和,还有一类隔一项的裂项求和,如![]() 或
或![]() .
.
【题型】解答题
【结束】
22
【题目】已知函数![]() 的图象上有两点
的图象上有两点![]() ,
,![]() .函数
.函数![]() 满足
满足![]() ,且
,且![]() .
.
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)能否保证![]() 和
和![]() 中至少有一个为正数?请证明你的结论.
中至少有一个为正数?请证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com