
科目: 来源: 题型:
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:
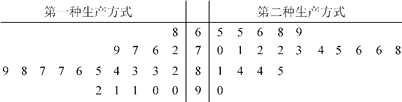
(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数![]() ,并将完成生产任务所需时间超过
,并将完成生产任务所需时间超过![]() 和不超过
和不超过![]() 的工人数填入下面的列联表:
的工人数填入下面的列联表:
超过 | 不超过 | |
第一种生产方式 | ||
第二种生产方式 |
(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?
附:![]() ,
,
|
|
|
|
|
|
|
|
查看答案和解析>>
科目: 来源: 题型:
【题目】某汽车公司对最近6个月内的市场占有率进行了统计,结果如表;
月份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
市场占有率 | 11 | 13 | 16 | 15 | 20 | 21 |
(1)可用线性回归模型拟合![]() 与
与![]() 之间的关系吗?如果能,请求出
之间的关系吗?如果能,请求出![]() 关于
关于![]() 的线性回归方程,如果不能,请说明理由;
的线性回归方程,如果不能,请说明理由;
(2)公司决定再采购![]() 两款车扩大市场,
两款车扩大市场, ![]() 两款车各100辆的资料如表:
两款车各100辆的资料如表:
车型 | 报废年限(年) | 合计 | 成本 | |||
1 | 2 | 3 | 4 | |||
| 10 | 30 | 40 | 20 | 100 | 1000元/辆 |
| 15 | 40 | 35 | 10 | 100 | 800元/辆 |
平均每辆车每年可为公司带来收入![]() 元,不考虑采购成本之外的其他成本,假设每辆车的使用寿命部是整数年,用每辆车使用寿命的频率作为概率,以每辆车产生利润的平均数作为决策依据,应选择采购哪款车型?
元,不考虑采购成本之外的其他成本,假设每辆车的使用寿命部是整数年,用每辆车使用寿命的频率作为概率,以每辆车产生利润的平均数作为决策依据,应选择采购哪款车型?
参考数据: ![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式:相关系数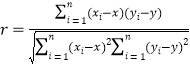 ;
;
回归直线方程为![]() ,其中
,其中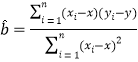 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市政府为了引导居民合理用水,决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价:若用水量不超过12吨时,按4元/吨计算水费;若用水量超过12吨且不超过14吨时,超过12吨部分按6.60元/吨计算水费;若用水量超过14吨时,超过14吨部分按7.80元/吨计算水费.为了了解全市居民月用水量的分布情况,通过抽样,获得了100户居民的月用水量(单位:吨),将数据按照[0,2],(2,4],…,(14,16]分成8组,制成了如图1所示的频率分布直方图. 
(Ⅰ)假设用抽到的100户居民月用水量作为样本估计全市的居民用水情况.
( i)现从全市居民中依次随机抽取5户,求这5户居民恰好3户居民的月用水用量都超过12吨的概率;
(ⅱ)试估计全市居民用水价格的期望(精确到0.01);
(Ⅱ)如图2是该市居民李某2016年1~6月份的月用水费y(元)与月份x的散点图,其拟合的线性回归方程是 ![]() .若李某2016年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
.若李某2016年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
查看答案和解析>>
科目: 来源: 题型:
【题目】在正整数数列中,由1开始按如下规则依次取它的项:第一次取1;第二次取2个连续偶数![]() ;第三次取3个连续奇数
;第三次取3个连续奇数![]() ;第四次取4个连续偶数
;第四次取4个连续偶数![]() ;第五次取5个连续奇数
;第五次取5个连续奇数![]() ;……按此规律取下去,得到一个子数列
;……按此规律取下去,得到一个子数列![]() ,
,![]() ,……则在这个子数列中,第
,……则在这个子数列中,第![]() 个数是( )
个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】给出下列四个命题:①命题“若![]() ,则
,则![]() ”的逆否命题为假命题:
”的逆否命题为假命题:
②命题“若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”;
”;
③若“![]() ”为真命题,“
”为真命题,“![]() ”为假命题,则
”为假命题,则![]() 为真命题,
为真命题,![]() 为假命题;
为假命题;
④函数![]() 有极值的充要条件是
有极值的充要条件是![]() 或
或![]() .
.
其中正确的个数有( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某地区有小学21所,中学14所,大学7所,现采取分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查。
(I)求应从小学、中学、大学中分别抽取的学校数目。
(II)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,
(1)列出所有可能的抽取结果;
(2)求抽取的2所学校均为小学的概率。
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,侧面PAD⊥底面ABCD,底面ABCD是平行四边形,∠ABC=45°,AD=AP=2, ![]() ,E为CD的中点,点F在线段PB上.
,E为CD的中点,点F在线段PB上. 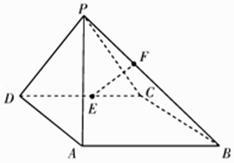
(Ⅰ)求证:AD⊥PC;
(Ⅱ)试确定点F的位置,使得直线EF与平面PDC所成的角和直线EF与平面ABCD所成的角相等.
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且B=60°,c=4.
(Ⅰ)若b=6,求角C的正弦值及△ABC的面积;
(Ⅱ)若D,E在线段BC上,且BD=DE=EC, ![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com