
科目: 来源: 题型:
【题目】某公司新上一条生产线,为保证新的生产线正常工作,需对该生产线进行检测,现从该生产线上随机抽取100件产品,测量产品数据,用统计方法得到样本的平均数![]() ,标准差
,标准差![]() ,绘制如图所示的频率分布直方图,以频率值作为概率估值。
,绘制如图所示的频率分布直方图,以频率值作为概率估值。

(1)从该生产线加工的产品中任意抽取一件,记其数据为![]() ,依据以下不等式评判(
,依据以下不等式评判(![]() 表示对应事件的概率)
表示对应事件的概率)
①![]()
②![]()
③![]()
评判规则为:若至少满足以上两个不等式,则生产状况为优,无需检修;否则需检修生产线,试判断该生产线是否需要检修;
(2)将数据不在![]() 内的产品视为次品,从该生产线加工的产品中任意抽取2件,次品数记为
内的产品视为次品,从该生产线加工的产品中任意抽取2件,次品数记为![]() ,求
,求![]() 的分布列与数学期望
的分布列与数学期望![]() 。
。
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=ex﹣1﹣ax(a>1)在[0,a]上的最小值为f(x0),且x0<2,则实数a的取值范围是( )
A.(1,2)
B.(1,e)
C.(2,e)
D.( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目: 来源: 题型:
【题目】某校200名学生的数学期中考试成绩频率分布直方图如图所示,其中成绩分组区间是![]() .
.
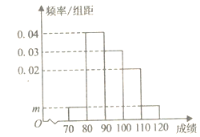
(1)求图中m的值;
(2)根据频率分布直方图,估计这200名学生的平均分(同一组中的数据用该组区间的中间值作代表)和中位数(四舍五入取整数);
(3)若这200名学生的数学成绩中,某些分数段的人数x与英语成绩相应分数段的人数y之比如下表所示,求英语成绩在![]() 的人数.
的人数.
分数段 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) |
x:y | 1:2 | 2:1 | 6:5 | 1:2 | 1:1 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆 ![]() (a>b>0)的左、右焦点分别为F1 , F2 , 过F1且与x轴垂直的直线交椭圆于A、B两点,直线AF2与椭圆的另一个交点为C,若△ABF2的面积是△BCF2的面积的2倍,则椭圆的离心率为( )
(a>b>0)的左、右焦点分别为F1 , F2 , 过F1且与x轴垂直的直线交椭圆于A、B两点,直线AF2与椭圆的另一个交点为C,若△ABF2的面积是△BCF2的面积的2倍,则椭圆的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】设甲、乙、丙三个乒乓球协会分别选派3,1,2名运动员参加某次比赛,甲协会运动员编号分别为![]() ,
,![]() ,
,![]() ,乙协会编号为
,乙协会编号为![]() ,丙协会编号分别为
,丙协会编号分别为![]() ,
,![]() ,若从这6名运动员中随机抽取2名参加双打比赛.
,若从这6名运动员中随机抽取2名参加双打比赛.
(1)用所给编号列出所有可能抽取的结果;
(2)求丙协会至少有一名运动员参加双打比赛的概率;
(3)求参加双打比赛的两名运动员来自同一协会的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】将函数f(x)=sin(2x+φ)+ ![]() cos(2x+φ)(0<φ<π)图象向左平移
cos(2x+φ)(0<φ<π)图象向左平移 ![]() 个单位后,得到函数的图象关于点(
个单位后,得到函数的图象关于点( ![]() ,0)对称,则函数g(x)=cos(x+φ)在[﹣
,0)对称,则函数g(x)=cos(x+φ)在[﹣ ![]() ,
, ![]() ]上的最小值是( )
]上的最小值是( )
A.﹣ ![]()
B.﹣ ![]()
C.![]()
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称函数
成立,则称函数![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数的上界.已知函数
称为函数的上界.已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的值域,并判断函数
上的值域,并判断函数![]() 在
在![]() 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数![]() 在
在![]() 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,函数
,函数![]() 在
在![]() 上的上界是
上的上界是![]() ,求
,求![]() 的解析式.
的解析式.
查看答案和解析>>
科目: 来源: 题型:
【题目】数学40名数学教师,按年龄从小到大编号为1,2,…40。现从中任意选取6人分成两组分配到A,B两所学校从事支教工作,其中三名编号较小的教师在一组,三名编号较大的教师在另一组,那么编号为8,12,28的数学教师同时入选并被分配到同一所学校的方法种数是
A. 220 B. 440 C. 255 D. 510
查看答案和解析>>
科目: 来源: 题型:
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为![]() =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是
A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(![]() ,
,![]() )
)
C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=alnx+x2+bx(a为实常数).
(1)若a=﹣2,b=﹣3,求f(x)的单调区间;
(2)若b=0,且a>﹣2e2 , 求函数f(x)在[1,e]上的最小值及相应的x值;
(3)设b=0,若存在x∈[1,e],使得f(x)≤(a+2)x成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com