
科目: 来源: 题型:
【题目】在等差数列{an}中,a3+a4+a5=84,a9=73.
(1)求数列{an}的通项公式;
(2)对任意m∈N* , 将数列{an}中落入区间(9m , 92m)内的项的个数记为bm , 求数列{bm}的前m项和Sm .
查看答案和解析>>
科目: 来源: 题型:
【题目】现有甲、乙两个靶.某射手向甲靶射击一次,命中的概率为 ![]() ,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为
,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为 ![]() ,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
(1)求该射手恰好命中一次得的概率;
(2)求该射手的总得分X的分布列及数学期望EX.
查看答案和解析>>
科目: 来源: 题型:
【题目】某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为![]() ,中奖可以获得2分;方案乙的中奖率为
,中奖可以获得2分;方案乙的中奖率为![]() ,中奖可以获得3分;未中奖则不得分。每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品。
,中奖可以获得3分;未中奖则不得分。每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品。
(Ⅰ)若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为![]() ,求
,求![]() 的概率;
的概率;
(Ⅱ)若小明、小红两人都选择方案甲或都选择方案乙进行抽奖,问:他们选择何种方案抽奖,累计得分的数学期望较大?
查看答案和解析>>
科目: 来源: 题型:
【题目】从甲、乙两名学生中选拔一人参加射箭比赛,为此需要对他们的射箭水平进行测试.现这两名学生在相同条件下各射箭10次,命中的环数如下:
甲 | 8 | 9 | 7 | 9 | 7 | 6 | 10 | 10 | 8 | 6 |
乙 | 10 | 9 | 8 | 6 | 8 | 7 | 9 | 7 | 8 | 8 |
(1)计算甲、乙两人射箭命中环数的平均数和标准差;
(2)比较两个人的成绩,然后决定选择哪名学生参加射箭比赛.
查看答案和解析>>
科目: 来源: 题型:
【题目】“中国人均读书![]() 本(包括网络文学和教科书),比韩国的
本(包括网络文学和教科书),比韩国的![]() 本、法国的
本、法国的![]() 本、日本的
本、日本的![]() 本、犹太人的
本、犹太人的![]() 本少得多,是世界上人均读书最少的国家”,这个论断被各种媒体反复引用.出现这样统计结果无疑是令人尴尬的,而且和其他国家相比,我国国民的阅读量如此之低,也和我国是传统的文明古国、礼仪之邦的地位不相符.某小区为了提高小区内人员的读书兴趣,特举办读书活动,准备进一定量的书籍丰富小区图书站,由于不同年龄段需看不同类型的书籍,为了合理配备资源,现对小区内看书人员进行年龄调查,随机抽取了一天
本少得多,是世界上人均读书最少的国家”,这个论断被各种媒体反复引用.出现这样统计结果无疑是令人尴尬的,而且和其他国家相比,我国国民的阅读量如此之低,也和我国是传统的文明古国、礼仪之邦的地位不相符.某小区为了提高小区内人员的读书兴趣,特举办读书活动,准备进一定量的书籍丰富小区图书站,由于不同年龄段需看不同类型的书籍,为了合理配备资源,现对小区内看书人员进行年龄调查,随机抽取了一天![]() 名读书者进行调查,将他们的年龄分成
名读书者进行调查,将他们的年龄分成![]() 段:
段:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 后得到如图所示的频率分布直方图.问:
后得到如图所示的频率分布直方图.问:

(1)估计在这![]() 名读书者中年龄分布在
名读书者中年龄分布在![]() 的人数;
的人数;
(2)求这![]() 名读书者年龄的平均数和中位数;
名读书者年龄的平均数和中位数;
(3)若从年龄在![]() 的读书者中任取
的读书者中任取![]() 名,求这两名读书者年龄在
名,求这两名读书者年龄在![]() 的人数恰为
的人数恰为![]() 的概率.
的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某生产企业研发了一种新产品,该产品在试销一个阶段后得到销售单价![]() (单位:元)和销售量
(单位:元)和销售量![]() (单位:万件)之间的一组数据,如下表所示:
(单位:万件)之间的一组数据,如下表所示:
销售单价 |
|
|
|
|
|
销售量 |
|
|
|
|
|
(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)从反馈的信息来看,消费者对该产品的心理价(单位:元/件)在![]() 内,已知该产品的成本是
内,已知该产品的成本是![]() 元,那么在消费者对该产品的心理价的范围内,销售单价定为多少时,企业才能获得最大利润?(注:利润=销售收入-成本)
元,那么在消费者对该产品的心理价的范围内,销售单价定为多少时,企业才能获得最大利润?(注:利润=销售收入-成本)
参考数据:![]()
参考公式: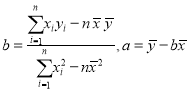
查看答案和解析>>
科目: 来源: 题型:
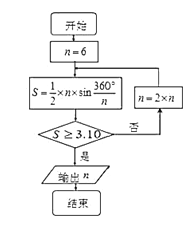
【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”,利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值![]() ,这就是著名的“徽率”,如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出
,这就是著名的“徽率”,如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出![]() 的值为 ( )
的值为 ( )
(参考数据:![]() )
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f (x)=x2,g(x)=x-1.
(1)若存在x∈R使f(x)<b·g(x),求实数b的取值范围;
(2)设F(x)=f(x)-mg(x)+1-m-m2,且|F(x)|在![]() 上单调递增,求实数m的取值范围.
上单调递增,求实数m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】在2007全运会上两名射击运动员甲、乙在比赛中打出如下成绩:
甲:9.4,8.7,7.5,8.4,10.1,10.5,10.7,7.2,7.8,10.8;
乙:9.1,8.7,7.1,9.8,9.7,8.5,10.1,9.2,10.1,9.1;
(1)用茎叶图表示甲,乙两个成绩;并根据茎叶图分析甲、乙两人成绩;
(2)分别计算两个样本的平均数![]() 和标准差
和标准差![]() ,并根据计算结果估计哪位运动员的成绩比较稳定.
,并根据计算结果估计哪位运动员的成绩比较稳定.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com