历年气象资料表明，该工程施工期间降水量X小于300，700，900的概率分别为0.3，0.7，0.9，求：
（1）工期延误天数Y的均值与方差；
（2）在降水量X至少是300的条件下，工期延误不超过6天的概率．

【题目】如图1，∠ACB=45°，BC=3，过动点A作AD⊥BC，垂足D在线段BC上且异于点B，连接AB，沿AD将△ABD折起，使∠BDC=90°（如图2所示），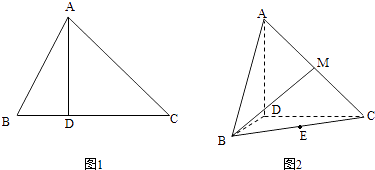

（1）当BD的长为多少时，三棱锥A﹣BCD的体积最大；
（2）当三棱锥A﹣BCD的体积最大时，设点E，M分别为棱BC，AC的中点，试在棱CD上确定一点N，使得EN⊥BM，并求EN与平面BMN所成角的大小．

【题目】北京某附属中学为了改善学生的住宿条件，决定在学校附近修建学生宿舍，学校总务办公室用1000万元从政府购得一块廉价土地，该土地可以建造每层1000平方米的楼房，楼房的每平方米建筑费用与建筑高度有关，楼房每升高一层，整层楼每平方米建筑费用提高0.02万元，已知建筑第5层楼房时，每平方米建筑费用为0.8万元．

（1）若学生宿舍建筑为层楼时，该楼房综合费用为万元，综合费用是建筑费用与购地费用之和），写出的表达式；

（2）为了使该楼房每平方米的平均综合费用最低，学校应把楼层建成几层？此时平均综合费用为每平方米多少万元？

【答案】（1）；（2）学校应把楼层建成层，此时平均综合费用为每平方米万元

【解析】

由已知求出第层楼房每平方米建筑费用为万元，得到第层楼房建筑费用，由楼房每升高一层，整层楼建筑费用提高万元，然后利用等差数列前项和求建筑层楼时的综合费用；

设楼房每平方米的平均综合费用为，则，然后利用基本不等式求最值．

解：由建筑第5层楼房时，每平方米建筑费用为万元，

且楼房每升高一层，整层楼每平方米建筑费用提高万元，

可得建筑第1层楼房每平方米建筑费用为：万元．

建筑第1层楼房建筑费用为：万元．

楼房每升高一层，整层楼建筑费用提高：万元．

建筑第x层楼时，该楼房综合费用为：．

；

设该楼房每平方米的平均综合费用为，

则：，

当且仅当，即时，上式等号成立．

学校应把楼层建成10层，此时平均综合费用为每平方米万元．

【点睛】

本题考查简单的数学建模思想方法，训练了等差数列前n项和的求法，训练了利用基本不等式求最值，是中档题．

【题型】解答题
【结束】
20

【题目】已知．

（1）求函数的最小正周期和对称轴方程；

（2）若，求的值域．

【题目】已知等差数列{an}前三项的和为﹣3，前三项的积为8．
（1）求等差数列{an}的通项公式；
（2）若a2 ， a3 ， a1成等比数列，求数列{|an|}的前n项和．

【题目】已知向量 =（cosωx﹣sinωx，sinωx）， =（﹣cosωx﹣sinωx，2 cosωx），设函数f（x）= +λ（x∈R）的图象关于直线x=π对称，其中ω，λ为常数，且ω∈（ ，1）
（1）求函数f（x）的最小正周期；
（2）若y=f（x）的图象经过点（ ，0）求函数f（x）在区间[0， ]上的取值范围．

【题目】（选修4﹣4：坐标系与参数方程）：
在直角坐标系xOy中，以原点O为极点，x轴的正半轴为极轴建立极坐标系，已知射线θ= 与曲线 （t为参数）相交于A，B来两点，则线段AB的中点的直角坐标为 ．

【题目】已知圆有以下性质：

①过圆上一点的圆的切线方程是.

②若不在坐标轴上的点为圆外一点，过作圆的两条切线，切点分别为，则垂直，即.

（1）类比上述有关结论，猜想过椭圆上一点的切线方程 (不要求证明)；

（2）若过椭圆外一点（不在坐标轴上）作两直线，与椭圆相切于两点，求证：为定值.

【题目】如图，双曲线 =1（a，b＞0）的两顶点为A1 ， A2 ， 虚轴两端点为B1 ， B2 ， 两焦点为F1 ， F2 ． 若以A1A2为直径的圆内切于菱形F1B1F2B2 ， 切点分别为A，B，C，D．则： （Ⅰ）双曲线的离心率e=；
（Ⅱ）菱形F1B1F2B2的面积S1与矩形ABCD的面积S2的比值 = ．

【题目】我国古代数学名著《九章算术》中“开立圆术”曰：置积尺数，以十六乘之，九而一，所得开立方除之，即立圆径，“开立圆术”相当于给出了已知球的体积V，求其直径d的一个近似公式d≈ ．人们还用过一些类似的近似公式．根据π=3.14159…..判断，下列近似公式中最精确的一个是（ ）
A.d≈
B.d≈
C.d≈
D.d≈

【题目】已知，则_____．

【答案】

【解析】

分子分母同时除以，把目标式转为的表达式，代入可求.

，则

故答案为：．

【点睛】

本题考查三角函数的化简求值，常用方法：(1)弦切互化法:主要利用公式, 形如等类型可进行弦化切；（2）“1”的灵活代换和的关系进行变形、转化.

【题型】填空题
【结束】
15

【题目】如图，正方体的棱长为1，为中点，连接，则异面直线和所成角的余弦值为_____．