
科目: 来源: 题型:
【题目】已知函数f(x)= ![]() +x.
+x.
(1)若函数f(x)的图象在(1,f(1))处的切线经过点(0,﹣1),求a的值;
(2)是否存在负整数a,使函数f(x)的极大值为正值?若存在,求出所有负整数a的值;若不存在,请说明理由;
(3)设a>0,求证:函数f(x)既有极大值,又有极小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某食品店为了了解气温对销售量的影响,随机记录了该店1月份中5天的日销售量![]() (单位:千克)与该地当日最低气温
(单位:千克)与该地当日最低气温![]() (单位:
(单位: ![]() )的数据,如下表:
)的数据,如下表:
| 2 | 5 | 8 | 9 | 11 |
| 12 | 10 | 8 | 8 | 7 |
(1)求出![]() 与
与![]() 的回归方程
的回归方程![]() ;
;
(2)判断![]() 与
与![]() 之间是正相关还是负相关;若该地1月份某天的最低气温为6
之间是正相关还是负相关;若该地1月份某天的最低气温为6![]() ,请用所求回归方程预测该店当日的营业额.
,请用所求回归方程预测该店当日的营业额.
附: 回归方程![]() 中,
中,  ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知过点![]() 的直线
的直线![]() 的参数方程是
的参数方程是 (
(![]() 为参数).以平面直角坐标系的原点为极点,
为参数).以平面直角坐标系的原点为极点, ![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程式为
的极坐标方程式为![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的右焦点为F,过点F的直线交y轴于点N,交椭圆C于点A、P(P在第一象限),过点P作y轴的垂线交椭圆C于另外一点Q.若
=1(a>b>0)的右焦点为F,过点F的直线交y轴于点N,交椭圆C于点A、P(P在第一象限),过点P作y轴的垂线交椭圆C于另外一点Q.若 ![]() .
. 
(1)设直线PF、QF的斜率分别为k、k',求证: ![]() 为定值;
为定值;
(2)若 ![]() 且△APQ的面积为
且△APQ的面积为 ![]() ,求椭圆C的方程.
,求椭圆C的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了监控某种零件的一条生产线的生产过程,检验员每隔30 min从该生产线上随机抽取一个零件,并测量其尺寸(单位:cm).下面是检验员在一天内依次抽取的16个零件的尺寸:
抽取顺序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
零件尺寸 | 9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
抽取次序 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
零件尺寸 | 10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得![]() =
=![]() xi=9.97,s=
xi=9.97,s=![]() =
=![]() ≈0.212,
≈0.212,![]() ≈18.439,
≈18.439,![]() (xi﹣
(xi﹣![]() )(i﹣8.5)=﹣2.78,
)(i﹣8.5)=﹣2.78,
其中xi为抽取的第i个零件的尺寸,i=1,2,…,16.
(1)求(xi,i)(i=1,2,…,16)的相关系数r,并回答是否可以认为这一天生产的零件尺寸不随生产
过程的进行而系统地变大或变小(若|r|<0.25,则可以认为零件的尺寸不随生产过程的进行而系统地
变大或变小).
(2)一天内抽检零件中,如果出现了尺寸在(![]() ﹣3s,
﹣3s,![]() +3s)之外的零件,就认为这条生产线在这一天
+3s)之外的零件,就认为这条生产线在这一天
的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
①从这一天抽检的结果看,是否需对当天的生产过程进行检查?
②在(![]() ﹣3s,
﹣3s,![]() +3s)之外的数据称为离群值,试剔除离群值,估计这条生产线当天生产的零件尺寸的
+3s)之外的数据称为离群值,试剔除离群值,估计这条生产线当天生产的零件尺寸的
均值与标准差.(精确到0.01)
附:样本(xi,yi)(i=1,2,…,n)的相关系数r=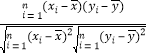 ,
,![]() ≈0.09.
≈0.09.
查看答案和解析>>
科目: 来源: 题型:
【题目】有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.
优秀 | 非优秀 | 总计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 | 105 |
已知在全部105人中随机抽取一人为优秀的概率为![]() .
.
(1)请完成上面的列联表;
(2)根据列联表的数据,若按97.5%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到10或11号的概率.
参考公式和数据: ![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某市在海岛A上建了一水产养殖中心.在海岸线l上有相距70公里的B、C两个小镇,并且AB=30公里,AC=80公里,已知B镇在养殖中心工作的员工有3百人,C镇在养殖中心工作的员工有5百人.现欲在BC之间建一个码头D,运送来自两镇的员工到养殖中心工作,又知水路运输与陆路运输每百人每公里运输成本之比为1:2. 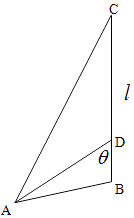
(1)求sin∠ABC的大小;
(2)设∠ADB=θ,试确定θ的大小,使得运输总成本最少.
查看答案和解析>>
科目: 来源: 题型:
【题目】以下资料是一位销售经理收集到的每年销售额y(千元)和销售经验x(年)的关系:
销售经验x/年 | 1 | 3 | 4 | 4 | 6 | 8 | 10 | 10 | 11 | 13 |
年销售额y/千元 | 80 | 97 | 92 | 102 | 103 | 111 | 119 | 123 | 117 | 136 |
(1)依据这些数据画出散点图并作直线![]() =78+4.2x,计算
=78+4.2x,计算![]() ;
;
(2)依据这些数据求回归直线方程并据此计算![]() ;
;
(3)比较(1) (2)中的残差平方和![]() 的大小.
的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆M:x2+y2﹣2x+a=0.
(1)若a=﹣8,过点P(4,5)作圆M的切线,求该切线方程;
(2)若AB为圆M的任意一条直径,且 ![]() =﹣6(其中O为坐标原点),求圆M的半径.
=﹣6(其中O为坐标原点),求圆M的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com