【题目】设函数f（x）=|3x﹣1|+ax+3，a∈R．
（1）若a=1，解不等式f（x）≤4；
（2）若函数f（x）有最小值，求a的取值范围．

【题目】在极坐标系中，圆C的方程为ρ=2acosθ（a≠0），以极点为坐标原点，极轴为x轴正半轴建立平面直角坐标系，设直线l的参数方程为 （t为参数）．
（1）求圆C的直角坐标方程（化为标准方程）和直线l的极坐标方程；
（2）若直线l与圆C只有一个公共点，且a＜1，求a的值．

【题目】如图，A，B，C，D四点在同一圆上，BC与AD的延长线交于点E，点F在BA的延长线上．

（1）若 = ， =1，求 的值；
（2）若EF2=FAFB，证明：EF∥CD．

【题目】已知函数f（x）=lnx﹣a（x﹣1），g（x）=ex ．
（1）当a=2时，求函数f（x）的最值；
（2）当a≠0时，过原点分别作曲线y=f（x）与y=g（x）的切线l1 ， l2 ， 已知两切线的斜率互为倒数，证明： ＜a＜ ．

【题目】已知函数．

（1）求函数在区间上的最大、最小值；

（2）求证：在区间上，函数的图象在函数的图象的下方．

【题目】如图，椭圆 =1（a＞b＞0）的左、右顶点分别为A，B，焦距为2 ，直线x=﹣a与y=b交于点D，且|BD|=3 ，过点B作直线l交直线x=﹣a于点M，交椭圆于另一点P．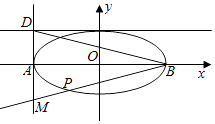

（1）求椭圆的方程；
（2）证明： 为定值．

(1)求曲线y＝f(x)在点(0，f(0))处的切线方程；

(2)求函数y＝f(x)的极值．

注：服务员在准备泡茶工具时的间隔时间忽略不计，并将频率视为概率．
（1）求服务员恰好在第6分钟开始准备第三位顾客的泡茶工具的概率；
（2）用X表示至第4分钟末已准备好了工具的顾客人数，求X的分布列及数学期望．

【题目】在如图所示的四棱锥P﹣ABCD中，四边形ABCD为正方形，PA⊥CD，BC⊥平面PAB，且E，M，N分别为PD，CD，AD的中点， =3 ．

（1）证明：PB∥平面FMN；
（2）若PA=AB，求二面角E﹣AC﹣B的余弦值．

A. 900元 B. 840元

C. 818元 D. 816元