【题目】如图，已知正三棱锥P﹣ABC的侧面是直角三角形，PA=6，顶点P在平面ABC内的正投影为点D，D在平面PAB内的正投影为点E，连接PE并延长交AB于点G．

（1）证明：G是AB的中点；
（2）在图中作出点E在平面PAC内的正投影F（说明作法及理由），并求四面体PDEF的体积．

【题目】已知正四棱柱ABCD﹣A1B1C1D1中，AA1=2AB，则CD与平面BDC1所成角的正弦值等于（ ）
A.
B.
C.
D.

【题目】已知函数.

（1）当时，探究函数的单调性；

（2）若关于的不等式在上恒成立，求的取值范围.

【题目】如图，正方体ABCD-A1B1C1D1的棱长为1，线段B1D1上有两个动点E，F，且EF= ， 则下列结论中错误的个数是( )

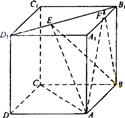
(1) AC⊥BE.
(2) 若P为AA1上的一点,则P到平面BEF的距离为.
(3) 三棱锥A-BEF的体积为定值.
(4) 在空间与DD1,AC,B1C1都相交的直线有无数条.
(5) 过CC1的中点与直线AC1所成角为40并且与平面BEF所成角为50的直线有2条.
A.0
B.1
C.2
D.3

（Ⅰ） 当a=﹣1时，求证：f（x）≤0；

（Ⅱ） 对任意x2≥ex1＞0，存在x∈（﹣1，+∞），使 成立，求a的取值范围．（其中e是自然对数的底数，e=2.71828…）

【题目】设A是由m×n个实数组成的m行n列的数表，满足：每个数的绝对值不大于1，且所有数的和为零，记s（m，n）为所有这样的数表构成的集合．对于A∈S（m，n），记ri（A）为A的第ⅰ行各数之和（1≤ⅰ≤m），Cj（A）为A的第j列各数之和（1≤j≤n）；记K（A）为|r1（A）|，|R2（A）|，…，|Rm（A）|，|C1（A）|，|C2（A）|，…，|Cn（A）|中的最小值．
（1）如表A，求K（A）的值；

（2）设数表A∈S（2，3）形如

求K（A）的最大值；
（3）给定正整数t，对于所有的A∈S（2，2t+1），求K（A）的最大值．

【题目】设函数，的图象在点处的切线与直线平行．

（1）求的值；

（2）若函数，且在区间上是单调函数，求实数的取值范围．

【题目】已知曲线C：（5﹣m）x2+（m﹣2）y2=8（m∈R）
（1）若曲线C是焦点在x轴点上的椭圆，求m的取值范围；
（2）设m=4，曲线c与y轴的交点为A，B（点A位于点B的上方），直线y=kx+4与曲线c交于不同的两点M、N，直线y=1与直线BM交于点G．求证：A，G，N三点共线．

(1)求a，b，c的值；

(2)先用分层抽样的方法从评定等级为“合格”和“不合格”的学生中随机抽取10人进行座谈，再从这10人中任选4人，记所选4人的量化总分为ξ，求ξ的分布列及数学期望E(ξ)；

(3)某评估机构以指标（，其中表示的方差）来评估该校开展安全教育活动的成效．若≥0.7，则认定教育活动是有效的；否则认定教育活动无效，应调整安全教育方案．在(2)的条件下，判断该校是否应调整安全教育方案．

【题目】已知函数f（x）=ax2+1（a＞0），g（x）=x3+bx
（1）若曲线y=f（x）与曲线y=g（x）在它们的交点（1，c）处具有公共切线，求a、b的值；
（2）当a2=4b时，求函数f（x）+g（x）的单调区间，并求其在区间（﹣∞，﹣1）上的最大值．