
科目: 来源: 题型:
【题目】已知点![]() 是圆
是圆![]() :
:![]() 上任意一点,点
上任意一点,点![]() 与点
与点![]() 关于原点对称,线段
关于原点对称,线段![]() 的垂直平分线与
的垂直平分线与![]() 交于
交于![]() 点.
点.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的动直线
的动直线![]() 与点
与点![]() 的轨迹交于
的轨迹交于![]() 两点,在
两点,在![]() 轴上是否存在定点
轴上是否存在定点![]() 使以
使以![]() 为直径的圆恒过这个点?若存在,求出点
为直径的圆恒过这个点?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】考拉兹猜想又名3n+1猜想,是指对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2.如此循环,最终都能得到1.阅读如图所示的程序框图,运行相应程序,输出的结果i=( ) 
A.4
B.5
C.6
D.7
查看答案和解析>>
科目: 来源: 题型:
【题目】我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水.天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积水深九寸,则平地降雨量是( )
(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸;③台体的体积公式V= ![]()
A.2寸
B.3寸
C.4寸
D.5寸
查看答案和解析>>
科目: 来源: 题型:
【题目】[选修4-5:不等式选讲]
已知函数f(x)=|x﹣m|﹣1.
(1)若不等式f(x)≤2的解集为{x|﹣1≤x≤5},求实数m的值;
(2)在(1)的条件下,若f(x)+f(x+5)≥t﹣2对一切实数x恒成立,求实数t的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】[选修4-4:极坐标与参数方程]
在直角坐标系xOy中,直线l的参数方程为 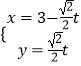 (t为参数).在极坐标系(与直角坐标系xOy取相同的长度单位),且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=4sinθ.
(t为参数).在极坐标系(与直角坐标系xOy取相同的长度单位),且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=4sinθ.
(1)求圆C的直角坐标方程和直线l普通方程;
(2)设圆C与直线l交于点A,B,若点P的坐标为(3,0),求|PA|+|PB|.
查看答案和解析>>
科目: 来源: 题型:
【题目】将参加夏令营的600名学生编号为:001,002,…,600,采用系统抽样的方法抽取一个容量为50的样本,且随机抽得的编号为003.这600名学生分住在3个营区,从001到300住在第1营区,从301到495住在第2营区,从496到600住在第3营区,则3个营区被抽中的人数依次为( )
A. 26,16,8 B. 25,16,9
C. 25,17,8 D. 24,17,9
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=lnx+bx﹣c,f(x)在点(1,f(1))处的切线方程为x+y+4=0.
(1)求f(x)的解析式;
(2)求f(x)的单调区间;
(3)若在区间 ![]() 内,恒有f(x)≥2lnx+kx成立,求k的取值范围.
内,恒有f(x)≥2lnx+kx成立,求k的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】从装有两个红球和两个黑球的口袋内任取两个球,那么互斥而不对立的两个事件是( )
A. “至少有一个黑球”与“都是红球”
B. “至少有一个黑球”与“至少有一个红球”
C. “至少有一个黑球”与“都是黑球”
D. “恰有一个黑球”与“恰有两个黑球”
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线的对称轴为坐标轴,顶点是坐标原点,准线方程为x=﹣1,直线l与抛物线相交于不同的A,B两点.
(1)求抛物线的标准方程;
(2)如果直线l过抛物线的焦点,求 ![]() 的值;
的值;
(3)如果 ![]() ,直线l是否过一定点,若过一定点,求出该定点;若不过一定点,试说明理由.
,直线l是否过一定点,若过一定点,求出该定点;若不过一定点,试说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】目前,学案导学模式已经成为教学中不可或缺的一部分,为了了解学案的合理使用是否对学生的期末复习有着重要的影响,我校随机抽取100名学生,对学习成绩和学案使用程度进行了调查,统计数据如表所示:
善于使用学案 | 不善于使用学案 | 总计 | |
学习成绩优秀 | 40 | ||
学习成绩一般 | 30 | ||
总计 | 100 |
参考公式: ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
参考数据:
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
已知随机抽查这100名学生中的一名学生,抽到善于使用学案的学生概率是0.6.
(1)请将上表补充完整(不用写计算过程);
(2)试运用独立性检验的思想方法分析:有多大的把握认为学生的学习成绩与对待学案的使用态度有关?
(3)利用分层抽样的方法从善于使用学案的同学中随机抽取6人,从这6人中抽出3人继续调查,设抽出学习成绩优秀的人数为X,求X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com