
【题目】目前,学案导学模式已经成为教学中不可或缺的一部分,为了了解学案的合理使用是否对学生的期末复习有着重要的影响,我校随机抽取100名学生,对学习成绩和学案使用程度进行了调查,统计数据如表所示:
善于使用学案 | 不善于使用学案 | 总计 | |
学习成绩优秀 | 40 | ||
学习成绩一般 | 30 | ||
总计 | 100 |
参考公式: ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
参考数据:
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
已知随机抽查这100名学生中的一名学生,抽到善于使用学案的学生概率是0.6.
(1)请将上表补充完整(不用写计算过程);
(2)试运用独立性检验的思想方法分析:有多大的把握认为学生的学习成绩与对待学案的使用态度有关?
(3)利用分层抽样的方法从善于使用学案的同学中随机抽取6人,从这6人中抽出3人继续调查,设抽出学习成绩优秀的人数为X,求X的分布列和数学期望.
【答案】
(1)解:
善于使用学案 | 不善于使用学案 | 总计 | |
学习成绩优秀 | 40 | 10 | 50 |
学习成绩一般 | 20 | 30 | 50 |
总计 | 60 | 40 | 100 |
(2)解:由上表可得:k2= ![]() =16,667>10.828,故有99.9%的把握认为学生的学习成绩与对待学案的使用态度有关
=16,667>10.828,故有99.9%的把握认为学生的学习成绩与对待学案的使用态度有关
(3)解:利用分层抽样的方法抽出成绩优秀的同学4人,一般的2人.从这6人中随机的抽出3人学习成绩优秀的人数X的取值为1,2,3.P(X=k)= ![]() ,则P(X=1)=
,则P(X=1)= ![]() ,P(X=2)=
,P(X=2)= ![]() ,P(X=3)=
,P(X=3)= ![]() .
.
其分布列为:
X | 1 | 2 | 3 |
P |
|
|
|
E(X)=1× ![]() +2×
+2× ![]() +3×
+3× ![]() =2
=2
【解析】(1.)
善于使用学案 | 不善于使用学案 | 总计 | |
学习成绩优秀 | 40 | 10 | 50 |
学习成绩一般 | 20 | 30 | 50 |
60 | 40 | 100 |
(2.)由上表可得:利用独立性检验公式可得k2 , 即可得出结论.(3)利用分层抽样的方法抽出成绩优秀的同学4人,一般的2人.从这6人中随机的抽出3人学习成绩优秀的人数X的取值为1,2,3.利用P(X=k)= ![]() 即可得出.
即可得出.
【考点精析】关于本题考查的离散型随机变量及其分布列,需要了解在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列才能得出正确答案.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
【题目】如图,将边长为2的正方体![]() 沿对角线
沿对角线![]() 折起,得到三棱锥
折起,得到三棱锥![]() ,则下列命题中,错误的为( )
,则下列命题中,错误的为( )
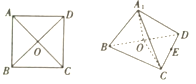
A. 直线![]() 平面
平面![]()
B. ![]()
C. 三棱锥![]() 的外接球的半径为
的外接球的半径为![]()
D. 若![]() 为
为![]() 的中点,则
的中点,则![]() 平面
平面![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() (
(![]() )的右焦点为
)的右焦点为![]() ,右顶点为
,右顶点为![]() ,已知
,已知![]() ,其中
,其中![]() 为原点,
为原点,![]() 为椭圆的离心率.
为椭圆的离心率.
(Ⅰ)求椭圆的方程;
(Ⅱ)设过点![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() ,求直线的
,求直线的![]() 斜率.
斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=![]() AD,∠BAD=∠ABC=90°,E是PD的中点.
AD,∠BAD=∠ABC=90°,E是PD的中点.
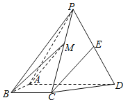
(1)证明:直线CE∥平面PAB;
(2)点M在棱PC上,且直线BM与底面ABCD所成角为45°,求二面角M-AB-D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校书法兴趣组有3名男同学A,B,C和3名女同学X,Y,Z,其年级情况如下表:
一年级 | 二年级 | 三年级 | |
男同学 | A | B | C |
女同学 | X | Y | Z |
现从这6名同学中随机选出2人参加书法比赛![]() 每人被选到的可能性相同
每人被选到的可能性相同![]() .
.
![]() 用表中字母列举出所有可能的结果;
用表中字母列举出所有可能的结果;
![]() 设M为事件“选出的2人来自不同年级且性别相同”,求事件M发生的概率.
设M为事件“选出的2人来自不同年级且性别相同”,求事件M发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:极坐标与参数方程]
在直角坐标系xOy中,直线l的参数方程为 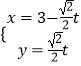 (t为参数).在极坐标系(与直角坐标系xOy取相同的长度单位),且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=4sinθ.
(t为参数).在极坐标系(与直角坐标系xOy取相同的长度单位),且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=4sinθ.
(1)求圆C的直角坐标方程和直线l普通方程;
(2)设圆C与直线l交于点A,B,若点P的坐标为(3,0),求|PA|+|PB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人进行某项对抗性游戏,采用“七局四胜”制,即先赢四局者为胜,若甲、乙两人水平相当,且已知甲先赢了前两局.
![]() Ⅰ
Ⅰ![]() 求乙取胜的概率;
求乙取胜的概率;
![]() Ⅱ
Ⅱ![]() 记比赛局数为X,求X的分布列及数学期望
记比赛局数为X,求X的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=|ax﹣2|.
(1)若关于x的不等式f(x)<3的解集为(﹣ ![]() ,
, ![]() ),求a的值;
),求a的值;
(2)f(x)+f(﹣x)≥a对于任意x∈R恒成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com