【题目】已知直线l： （t为参数，α为l的倾斜角），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C为：ρ2﹣6ρcosθ+5=0．
（1）若直线l与曲线C相切，求α的值；
（2）设曲线C上任意一点的直角坐标为（x，y），求x+y的取值范围．

【题目】种植于道路两侧、为车辆和行人遮阴并构成街景的乔木称为行道树为确保行人、车辆和临近道路附属设施安全，树木与原有电力线之间的距离不能超出安全距离按照北京市行道树修剪规范要求，当树木与原有电力线发生矛盾时，应及时修剪树枝行道树修剪规范中规定，树木与原有电力线的安全距离如表所示：树木与电力线的安全距离表

现有某棵行道树已经自然生长2年，高度为据研究，这种行道树自然生长的时间年与它的高度满足关系式

1______；将结果直接填写在答题卡的相应位置上

2如果这棵行道树的正上方有35kV的电力线，该电力线距地面那么这棵行道树自然生长多少年必须修剪？

3假如这棵行道树的正上方有500KV的电力线，这棵行道树一直自然生长，始终不会影响电力线段安全，那么该电力线距离地面至少多少米？

【题目】已知圆O：经过点，与x轴正半轴交于点B．

Ⅰ______；将结果直接填写在答题卡的相应位置上

Ⅱ圆O上是否存在点P，使得的面积为15？若存在，求出点P的坐标；若不存在，说明理由．

【题目】已知函数 ，a∈R．
（1）求函数f（x）的单调区间；
（2）若函数f（x）有两个零点x1 ， x2 ， （x1＜x2），求证：1＜x1＜a＜x2＜a2 ．

【题目】北京故宫博物院成立于1925年10月10日，是在明、清朝两代皇宫及其宫廷收藏的基础上建立起来的中国综合性博物馆，每年吸引着大批游客参观游览下图是从2012年到2017年每年参观人数的折线图根据图中信息，下列结论中正确的是　　

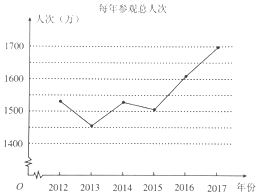
A. 2013年以来，每年参观总人次逐年递增

B. 2014年比2013年增加的参观人次不超过50万

C. 2012年到2017年这六年间，2017年参观总人次最多

D. 2012年到2017年这六年间，平均每年参观总人次超过160万

【题目】已知椭圆 （a＞b＞0）的一个顶点为B（0，4），离心率e= ，直线l交椭圆于M，N两点．
（1）若直线l的方程为y=x﹣4，求弦MN的长；
（2）如果△BMN的重心恰好为椭圆的右焦点F，求直线l方程的一般式．

【题目】北京市环境保护监测中心每月向公众公布北京市各区域的空气质量状况年1月份各区域的浓度情况如表：

各区域1月份浓度单位：微克立方米表

从上述表格随机选择一个区域，其2018年1月份的浓度小于36微克立方米的概率是　　

A. B. C. D.

【题目】某闯关游戏有这样一个环节：该关卡有一道上了锁的门，要想通过该关卡，要拿到门前密码箱里的钥匙，才能开门过关．但是密码箱需要一个密码才能打开，并且3次密码尝试错误，该密码箱被锁定，从而闯关失败．某人到达该关卡时，已经找到了可能打开密码箱的6个密码（其中只有一个能打开密码箱），他决定从中随机地选择1个密码进行尝试．若密码正确，则通关成功；否则继续尝试，直至密码箱被锁定．
（1）求这个人闯关失败的概率；
（2）设该人尝试密码的次数为X，求X的分布列和数学期望．

【题目】如图，已知四棱锥P﹣ABCD的底面为菱形，∠BCD=120°，AB=PC=2，AP=BP= ．

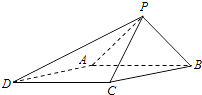
（1）求证：AB⊥PC；
（2）求二面角B一PC﹣D的余弦值．

【题目】已知椭圆上一点与椭圆右焦点的连线垂直于x轴，直线l：y＝kx＋m与椭圆C相交于A，B两点(均不在坐标轴上)．

(1)求椭圆C的标准方程；

(2)设O为坐标原点，若△AOB的面积为，试判断直线OA与OB的斜率之积是否为定值？若是请求出，若不是请说明理由．