【题目】已知直线l的参数方程为 （t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为2ρ2﹣ρ2cos2θ=12．若曲线C的左焦点F在直线l上，且直线l与曲线C交于A，B两点．
（1）求m的值并写出曲线C的直角坐标方程；
（2）求 的值．

【题目】已知函数f（x）=xex﹣a（lnx+x）．
（1）若函数f（x）恒有两个零点，求a的取值范围；
（2）若对任意x＞0，恒有不等式f（x）≥1成立． ①求实数a的值；
②证明：x2ex＞（x+2）lnx+2sinx．

【题目】已知椭圆 的离心率为 ，四个顶点构成的菱形的面积是4，圆M：（x+1）2+y2=r2（0＜r＜1）．过椭圆C的上顶点A作圆M的两条切线分别与椭圆C相交于B，D两点（不同于点A），直线AB，AD的斜率分别为k1 ， k2 ．
（1）求椭圆C的方程；
（2）当r变化时，①求k1k2的值；②试问直线BD是否过某个定点？若是，求出该定点；若不是，请说明理由．

【题目】随着生活水平和消费观念的转变，“三品一标”（无公害农产品、绿色食品、有机食品和农产品地理标志）已成为不少人的选择，为此某品牌植物油企业成立了有机食品快速检测室，假设该品牌植物油每瓶含有机物A的概率为p（0＜p＜1），需要通过抽取少量油样化验来确定该瓶油中是否含有有机物A，若化验结果呈阳性则含A，呈阴性则不含A．若多瓶该种植物油检验时，可逐个抽样化验，也可将若干瓶植物油的油样混在一起化验，仅当至少有一瓶油含有有机物A时混合油样呈阳性，若混合油样呈阳性，则该组植物油必须每瓶重新抽取油样并全部逐个化验．
（1）若 ，试求3瓶该植物油混合油样呈阳性的概率；
（2）现有4瓶该种植物油需要化验，有以下两种方案： 方案一：均分成两组化验；方案二：混在一起化验；请问哪种方案更适合（即化验次数的期望值更小），并说明理由．

【题目】如图，三棱柱ABC﹣A1B1C1中，∠ACB=90°，CC1⊥底面ABC，AC=BC=CC1=2，D，E，F分别是棱AB，BC，B1C1的中点，G是棱BB1上的动点．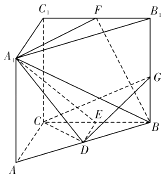
（1）当 为何值时，平面CDG⊥平面A1DE？
（2）求平面AB1F与平面AD1E所成的锐二面角的余弦值．

【题目】某学校的平面示意图为如下图五边形区域ABCDE，其中三角形区域ABE为生活区，四边形区域BCDE为教学区，AB，BC，CD，DE，EA，BE为学校的主要道路（不考虑宽度）. ， ．
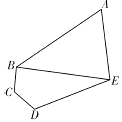
（1）求道路BE的长度；
（2）求生活区△ABE面积的最大值．

【题目】如图，某机械厂要将长，宽的长方形铁皮进行裁剪．已知点为的中点，点在边上，裁剪时先将四边形沿直线翻折到处（点分别落在直线下方点处，交边于点），再沿直线裁剪．

（1）当时，试判断四边形的形状，并求其面积；

（2）若使裁剪得到的四边形面积最大，请给出裁剪方案，并说明理由．

【题目】一个总体分为A，B两层，其个体数之比为5：1，用分层抽样方法从总体中抽取一个容量为12的样本，已知B层中甲、乙都被抽到的概率为 ，则总体中的个数为 ．

【题目】若函数f（x）=asinωx+bcosωx（0＜ω＜5，ab≠0）的图象的一条对称轴方程是 ，函数f'（x）的图象的一个对称中心是 ，则f（x）的最小正周期是（ ）
A.
B.
C.π
D.2π

【题目】设函数 ，则关于函数f（x）有以下四个命题（ ）
①x∈R，f（f（x））=1；
②x0 ， y0∈R，f（x0+y0）=f（x0）+f（y0）；
③函数f（x）是偶函数；
④函数f（x）是周期函数．
其中真命题的个数是（ ）
A.4
B.3
C.2
D.1