【题目】某校随机调查80名学生，以研究学生爱好羽毛球运动与性别的关系，得到下面的列联表：

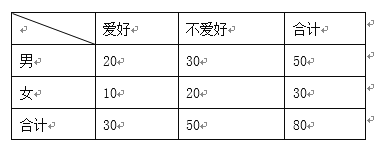
（1）将此样本的频率视为总体的概率，随机调查本校的3名学生，设这3人中爱好羽毛球运动的人数为，求的分布列和数学期望；

（2）根据表3中数据，能否认为爱好羽毛球运动与性别有关？

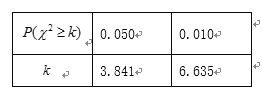
附：

【题目】若数列满足：，则称数列为“正弦数列”，现将这五个数排成一个“正弦数列”，所有排列种数记为，则二项式的展开式中含项的系数为________．

【题目】奇函数f（x）定义域是（﹣1，0）∪（0，1），f（）＝0，当x＞0时，总有（x）f′（x）ln（1﹣x2）＞2f（x）成立，则不等式f（x）＞0的解集为（　　）

A. B.

C. D.

【题目】类比三角形中的性质：（1）两边之和大于第三边；（2）中位线长等于底边的一半；（3）三内角平分线交于一点； 可得四面体的对应性质：（1）任意三个面的面积之和大于第四个面的面积；（2）过四面体的交于同一顶点的三条棱的中点的平面面积等于第四个面面积的；（3）四面体的六个二面角的平分面交于一点。其中类比推理结论正确的有 ( )

A. （1） B. （1）（2） C. （1）（2）（3） D. 都不对

【题目】设函数f（x）=lnx﹣ax2+ax，a为正实数．
（1）当a=2时，求曲线y=f（x）在点（1，f（1））处的切线方程；
（2）求证：f（ ）≤0；
（3）若函数f（x）有且只有1个零点，求a的值．

【题目】在数列{an}中，已知a1= ，an+1= an﹣ ，n∈N* ， 设Sn为{an}的前n项和．
（1）求证：数列{3nan}是等差数列；
（2）求Sn；
（3）是否存在正整数p，q，r（p＜q＜r），使Sp ， Sq ， Sr成等差数列？若存在，求出p，q，r的值；若不存在，说明理由．

【题目】某城市有一直角梯形绿地ABCD，其中∠ABC=∠BAD=90°，AD=DC=2km，BC=1km．现过边界CD上的点E处铺设一条直的灌溉水管EF，将绿地分成面积相等的两部分．

（1）如图①，若E为CD的中点，F在边界AB上，求灌溉水管EF的长度；
（2）如图②，若F在边界AD上，求灌溉水管EF的最短长度．

【题目】如图，在平面直角坐标系xOy中，已知圆C：x2+y2﹣4x=0及点A（﹣1，0），B（1，2）

（1）若直线l平行于AB，与圆C相交于M，N两点，MN=AB，求直线l的方程；
（2）在圆C上是否存在点P，使得PA2+PB2=12？若存在，求点P的个数；若不存在，说明理由．

【题目】已知函数在上单调递减，则实数的取值范围是（ ）

A. B. C. D.