
科目: 来源: 题型:
【题目】要测量电视塔AB的高度,在C点测得塔顶的仰角是45°,在D点测得塔顶的仰角是30°,并测得水平面上的∠BCD=120°,CD=40m,则电视塔的高度是( )
A.30m
B.40m
C.![]() m
m
D.![]() m
m
查看答案和解析>>
科目: 来源: 题型:
【题目】已知定义在R上的偶函数f(x)在[0,+∞)上递减,若不等式f(x3﹣x2+a)+f(﹣x3+x2﹣a)≥2f(1)对x∈[0,1]恒成立,则实数a的取值范围为( )
A.[ ![]() ,1]
,1]
B.[﹣ ![]() ,1]
,1]
C.[1,3]
D.(﹣∞,1]
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|≤ ![]() ),x=﹣
),x=﹣ ![]() 为f(x)的零点,x=
为f(x)的零点,x= ![]() 为y=f(x)图象的对称轴,且f(x)在(
为y=f(x)图象的对称轴,且f(x)在( ![]() ,
, ![]() )上单调,则ω的最大值为( )
)上单调,则ω的最大值为( )
A.11
B.9
C.7
D.5
查看答案和解析>>
科目: 来源: 题型:
【题目】[选修4-5:不等式选讲]
已知函数f(x)=|ax﹣2|.
(Ⅰ)当a=2时,解不等式f(x)>x+1;
(Ⅱ)若关于x的不等式f(x)+f(﹣x)< ![]() 有实数解,求m的取值范围.
有实数解,求m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】[选修4-4:坐标系与参数方程选讲]
在平面直角坐标系xOy中,以原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C1 , C2的极坐标方程分别为ρ=2sinθ,ρcos(θ﹣ ![]() )=
)= ![]() .
.
(Ⅰ)求C1和C2交点的极坐标;
(Ⅱ)直线l的参数方程为:  (t为参数),直线l与x轴的交点为P,且与C1交于A,B两点,求|PA|+|PB|.
(t为参数),直线l与x轴的交点为P,且与C1交于A,B两点,求|PA|+|PB|.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=x2﹣alnx(a>0)的最小值是1.
(Ⅰ)求a;
(Ⅱ)若关于x的方程f2(x)ex﹣6mf(x)+9me﹣x=0在区间[1,+∞)有唯一的实根,求m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知F为抛物线E:x2=2py(p>0)的焦点,直线l:y=kx+ ![]() 交抛物线E于A,B两点.
交抛物线E于A,B两点.
(Ⅰ)当k=1,|AB|=8时,求抛物线E的方程;
(Ⅱ)过点A,B作抛物线E的切线l1 , l2 , 且l1 , l2交点为P,若直线PF与直线l斜率之和为﹣ ![]() ,求直线l的斜率.
,求直线l的斜率.
查看答案和解析>>
科目: 来源: 题型:
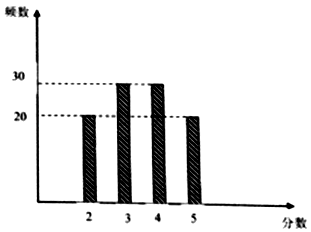
【题目】某校后勤处为跟踪调查该校餐厅的当月的服务质量,兑现奖惩,从就餐的学生中随机抽出100位学生对餐厅服务质量打分(5分制),得到如图柱状图.
(Ⅰ)从样本中任意选取2名学生,求恰好有1名学生的打分不低于4分的概率;
(Ⅱ)若以这100人打分的频率作为概率,在该校随机选取2名学生进行打分(学生打分之间相互独立)记X表示两人打分之和,求X的分布列和E(X).
(Ⅲ)根据(Ⅱ)的计算结果,后勤处对餐厅服务质量情况定为三个等级,并制定了对餐厅相应的奖惩方案,如表所示,设当月奖金为Y(单位:元),求E(Y).
服务质量评分X | X≤5 | 6≤X≤8 | X≥9 |
等级 | 不好 | 较好 | 优良 |
奖惩标准(元) | ﹣1000 | 2000 | 3000 |
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在五棱锥P﹣ABCDE中,△ABE是等边三角形,四边形BCDE是直角梯形且∠DEB=∠CBE=90°,G是CD的中点,点P在底面的射影落在线段AG上.
(Ⅰ)求证:平面PBE⊥平面APG;
(Ⅱ)已知AB=2,BC= ![]() ,侧棱PA与底面ABCDE所成角为45°,S△PBE=
,侧棱PA与底面ABCDE所成角为45°,S△PBE= ![]() ,点M在侧棱PC上,CM=2MP,求二面角M﹣AB﹣D的余弦值.
,点M在侧棱PC上,CM=2MP,求二面角M﹣AB﹣D的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知a,b分别是△ABC内角A,B的对边,且bsin2A= ![]() acosAsinB,函数f(x)=sinAcos2x﹣sin2
acosAsinB,函数f(x)=sinAcos2x﹣sin2 ![]() sin 2x,x∈[0,
sin 2x,x∈[0, ![]() ].
].
(Ⅰ)求A;
(Ⅱ)求函数f(x)的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com