【题目】如图，四边形 为菱形，四边形 为平行四边形，设 与 相交于点 ， ．

（1）证明：平面 平面 ；
（2）若 ，求三棱锥 的体积．

【题目】若 在 上存在最小值，则实数 的取值范围是（ ）
A.
B.
C.
D.

A.
B.
C.
D.π（4-h2）

【题目】设函数f（x）=|x﹣a|+5x．
（1）当a=﹣1时，求不等式f（x）≤5x+3的解集；
（2）若x≥﹣1时有f（x）≥0，求a的取值范围．

【题目】在平面直角坐标中，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，已知曲线C的极坐标方程为ρsin2θ=2acosθ（a＞0），直线l的参数方程为 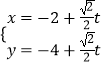（t为参数），直线l与曲线C相交于A，B两点．
（1）写出曲线C的直角坐标方程和直线l的普通方程；
（2）若|AB|=2 ，求a的值．

【题目】已知函数f（x）=xe2x﹣lnx﹣ax．
（1）当a=0时，求函数f（x）在[ ，1]上的最小值；
（2）若x＞0，不等式f（x）≥1恒成立，求a的取值范围；
（3）若x＞0，不等式f（ ）﹣1≥ e + 恒成立，求a的取值范围．

【题目】设椭圆E的方程为 +y2=1（a＞1），O为坐标原点，直线l与椭圆E交于点A，B，M为线段AB的中点．
（1）若A，B分别为E的左顶点和上顶点，且OM的斜率为﹣ ，求E的标准方程；
（2）若a=2，且|OM|=1，求△AOB面积的最大值．

【题目】某中学举行了一次“环保知识竞赛”活动．为了了解本次竞赛学生成绩情况，从中抽取了部分学生的分数（得分取正整数，满分为100分）作为样本（样本容量为n）进行统计．按照[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出频率分布直方图，并作出样本分数的茎叶图（图中仅列出了得分在[50，60），[90，100]的数据）．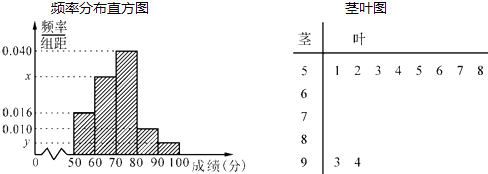
（Ⅰ）求样本容量n和频率分布直方图中x、y的值；
（Ⅱ）在选取的样本中，从竞赛成绩是80分以上（含80分）的同学中随机抽取3名同学到市政广场参加环保知识宣传的志愿者活动，设ξ表示所抽取的3名同学中得分在[80，90）的学生个数，求ξ的分布列及其数学期望．

【题目】数列{an}满足a1=1，nan+1=（n+1）an+n（n+1），n∈N* ． （Ⅰ）证明：数列{ }是等差数列；
（Ⅱ）设bn=3n ，求数列{bn}的前n项和Sn ．

【题目】在△ABC中，角A，B，C的对边分别是a，b，c，且 acosC=（2b﹣ c）cosA．
（1）求角A的大小；
（2）求cos（ ﹣B）﹣2sin2 的取值范围．