【题目】函数p（x）=lnx+x﹣4，q（x）=axex（a∈R）．
（Ⅰ）若a=e，设f（x）=p（x）﹣q（x），试证明f′（x）存在唯一零点x0∈（0， ），并求f（x）的最大值；
（Ⅱ）若关于x的不等式|p（x）|＞q（x）的解集中有且只有两个整数，求实数a的取值范围．

【题目】已知点E（﹣2，0），点P时圆F：（x﹣2）2+y2=36上任意一点，线段EP的垂直平分线交FP于点M，点M的轨迹记为曲线C．
（Ⅰ）求曲线C的方程；
（Ⅱ）过F的直线交曲线C于不同的A、B两点，交y轴于点N，已知 =m ， =n ，求m+n的值．

【题目】已知矩形ADEF和菱形ABCD所在平面互相垂直，如图，其中AF=1，AD=2，∠ADC= ，点N时线段AD的中点．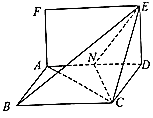
（Ⅰ）试问在线段BE上是否存在点M，使得直线AF∥平面MNC？若存在，请证明AF∥平面MNC，并求出 的值，若不存在，请说明理由；
（Ⅱ）求二面角N﹣CE﹣D的正弦值．

【题目】共享单车进驻城市，绿色出行引领时尚，某市有统计数据显示，2016年该市共享单车用户年龄等级分布如图1所示，一周内市民使用单车的频率分布扇形图如图2所示，若将共享单车用户按照年龄分为“年轻人”（20岁～39岁）和“非年轻人”（19岁及以下或者40岁及以上）两类，将一周内使用的次数为6次或6次以上的称为“经常使用单车用户”，使用次数为5次或不足5次的称为“不常使用单车用户”，已知在“经常使用单车用户”中有 是“年轻人”．
（Ⅰ）现对该市市民进行“经常使用共享单车与年龄关系”的调查，采用随机抽样的方法，抽取一个容量为200的样本，请你根据图表中的数据，补全下列2×2列联表，并根据列联表的独立性检验，判断能有多大把握可以认为经常使用共享单车与年龄有关？
使用共享单车情况与年龄列联表

（Ⅱ）将频率视为概率，若从该市市民中随机任取3人，设其中经常使用共享单车的“非年轻人”人数为随机变量X，求X的分布列与期望．
（参考数据：

其中，K2= ，n=a+b+c+d）

【题目】在△ABC中，a，b，c分别是内角A，B，C的对边，且（a+c）2=b2+3ac．
（Ⅰ）求角B的大小；
（Ⅱ）若b=2，且sinB+sin（C﹣A）=2sin2A，求△ABC的面积．

【题目】已知函数f（x）=2lnx﹣ax2+3，若存在实数m、n∈[1，5]满足n﹣m≥2时，f（m）=f（n）成立，则实数a的最大值为（ ）
A.
B.
C.
D.

【题目】三棱锥P﹣ABC中，PA、PB、PC互相垂直，PA=PB=1，M是线段BC上一动点，若直线AM与平面PBC所成角的正切的最大值是 ，则三棱锥P﹣ABC的外接球的表面积是（ ）
A.2π
B.4π
C.8π
D.16π

【题目】已知函数f（x）= mcos2x+（m﹣2）sinx，其中1≤m≤2，若函数f（x）的最大值记为g（m），则g（m）的最小值为（ ）
A.﹣
B.1
C.3﹣
D. ﹣1

【题目】在如图所示的程序框图中，若函数f（x）= ，则输出的结果是（ ）
A.16
B.8
C.216
D.28