
科目: 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,四边形ABCD是直角梯形,AB⊥AD,AB∥CD,
PC⊥底面ABCD,AB=2AD=2CD=4,PC=2a,E是PB的中点.
(Ⅰ)求证:平面EAC⊥平面PBC;
(Ⅱ)若二面角P﹣AC﹣E的余弦值为 ![]() ,求直线PA与平面EAC所成角的正弦值.
,求直线PA与平面EAC所成角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为 ![]() ,中奖可以获得2分;方案乙的中奖率为
,中奖可以获得2分;方案乙的中奖率为 ![]() ,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
(1)若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为x,求x≤3的概率;
(2)若小明、小红两人都选择方案甲或都选择方案乙进行抽奖,问:他们选择何种方案抽奖,累计得分的数学期望较大?
查看答案和解析>>
科目: 来源: 题型:
【题目】在某次试验中,有两个试验数据![]() ,统计的结果如下面的表格1.
,统计的结果如下面的表格1.
(1)在给出的坐标系中画出![]() 的散点图; 并判断正负相关;
的散点图; 并判断正负相关;
(2)填写表格2,然后根据表格2的内容和公式求出![]() 对
对![]() 的回归直线方程
的回归直线方程![]() ,并估计当
,并估计当![]() 为10时
为10时![]() 的值是多少?(公式:
的值是多少?(公式: ,
,![]() )
)
| 1 | 2 | 3 | 4 | 5 |
| 2 | 3 | 4 | 4 | 5 |
表1

表格2
序号 | | | | |
1 | 1 | 2 | ||
2 | 2 | 3 | ||
3 | 3 | 4 | ||
4 | 4 | 4 | ||
5 | 5 | 5 | ||
|
|
|
|
查看答案和解析>>
科目: 来源: 题型:
【题目】设数列{an}满足:a1=1,an+1=3an , n∈N* . 设Sn为数列{bn}的前n项和,已知b1≠0,2bn﹣b1=S1Sn , n∈N*
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)设cn=bnlog3an , 求数列{cn}的前n项和Tn;
(Ⅲ)证明:对任意n∈N*且n≥2,有 ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点P为函数f(x)=lnx的图象上任意一点,点Q为圆[x﹣(e+ ![]() )]2+y2=1任意一点,则线段PQ的长度的最小值为( )
)]2+y2=1任意一点,则线段PQ的长度的最小值为( )
A.![]()
B.![]()
C.![]()
D.e+ ![]() ﹣1
﹣1
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学随机选取了![]() 名男生,将他们的身高作为样本进行统计,得到如图所示的频率分布直方图,观察图中数据,完成下列问题.
名男生,将他们的身高作为样本进行统计,得到如图所示的频率分布直方图,观察图中数据,完成下列问题.
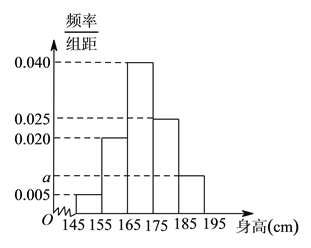
(![]() )求
)求![]() 的值及样本中男生身高在
的值及样本中男生身高在![]() (单位:
(单位:![]() )的人数.
)的人数.
(![]() )假设用一组中的每个数据可用该组区间的中点值代替,通过样本估计该校全体男生的平均身高.
)假设用一组中的每个数据可用该组区间的中点值代替,通过样本估计该校全体男生的平均身高.
(![]() )在样本中,从身高在
)在样本中,从身高在![]() 和
和![]() (单位:
(单位:![]() )内的男生中任选两人,求这两人的身高都不低于
)内的男生中任选两人,求这两人的身高都不低于![]() 的概率.
的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知定义在R上的函数y=f(x)满足:①对于任意的x∈R,都有f(x+2)=f(x﹣2);②函数y=f(x+2)是偶函数;③当x∈(0,2]时,f(x)=ex﹣ ![]() ,a=f(﹣5),b=f(
,a=f(﹣5),b=f( ![]() ).c=f(
).c=f( ![]() ),则a,b,c的大小关系是( )
),则a,b,c的大小关系是( )
A.a<b<c
B.c<a<b
C.c<a<b
D.b<a<c
查看答案和解析>>
科目: 来源: 题型:
【题目】将三颗骰子各掷一次,记事件A=“三个点数都不同”,B=“至少出现一个6点”,则条件概率P(A|B),P(B|A)分别是( )
A.![]() ,
, ![]()
B.![]() ,
, ![]()
C.![]() ,
, ![]()
D.![]() ,
, ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】下列命题中正确命题的个数是( ) ①对于命题p:x∈R,使得x2+x+1<0,则¬p:x∈R,均有x2+x+1>0;
②命题“已知x,y∈R,若x+y≠3,则x≠2或y≠1”是真命题;
③回归直线的斜率的估计值为1.23,样本点的中心为(4,5),则回归直线方程为 ![]() =1.23x+0.08;
=1.23x+0.08;
④m=3是直线(m+3)x+my﹣2=0与直线mx﹣6y+5=0互相垂直的充要条件.
A.1
B.3
C.2
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com