
科目: 来源: 题型:
【题目】已知椭圆 ![]() 的右焦点与抛物线y2=4x的焦点F重合,且椭圆的离心率是
的右焦点与抛物线y2=4x的焦点F重合,且椭圆的离心率是 ![]() ,如图所示.
,如图所示.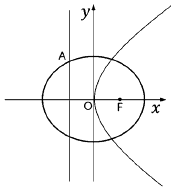
(1)求椭圆的标准方程;
(2)抛物线的准线与椭圆在第二象限相交于点A,过点A作抛物线的切线l,l与椭圆的另一个交点为B,求线段AB的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】在四棱锥P﹣ABCD中,DA⊥平面PAB,DC∥AB,DA=DC=2,AB=AP=4,∠PAB=120°,M为PB中点.
(Ⅰ)求证:CM∥平面PAD;
(Ⅱ)求二面角M﹣AC﹣B的余弦值.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知直三棱柱ABC﹣A1B1C1的所有棱长都相等,D,E分别是AB,A1C1的中点,如图所示. 
(1)求证:DE∥平面BCC1B1;
(2)求DE与平面ABC所成角的正切值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某职业学校的王亮同学到一家贸易公司实习,恰逢该公司要通过海运出口一批货物,王亮同学随公司负责人到保险公司洽谈货物运输期间的投保事宜,保险公司提供了缴纳保险费的两种方案:
①一次性缴纳50万元,可享受9折优惠;
②按照航行天数交纳:第一天缴纳0.5元,从第二天起每天交纳的金额都是其前一天的2倍,共需交纳20天.
请通过计算,帮助王亮同学判断那种方案交纳的保费较低.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=log2(3+x)﹣log2(3﹣x),
(1)求函数f(x)的定义域,并判断函数f(x)的奇偶性;
(2)已知f(sinα)=1,求α的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】从甲、乙、丙、丁四位同学中选拔一位成绩较稳定的优秀选手,参加山东省职业院校技能大赛,在同样条件下经过多轮测试,成绩分析如表所示,根据表中数据判断,最佳人选为( ) 成绩分析表
甲 | 乙 | 丙 | 丁 | |
平均成绩 | 96 | 96 | 85 | 85 |
标准差s | 4 | 2 | 4 | 2 |
A.甲
B.乙
C.丙
D.丁
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=ex﹣ax有极值1,这里e是自然对数的底数.
(1)求实数a的值,并确定1是极大值还是极小值;
(2)若当x∈[0,+∞)时,f(x)≥mxln(x+1)+1恒成立,求实数m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线C:x2=2py(p>0)的焦点为F,A为C上异于原点的任意一点,点A到x轴的距离等于|AF|﹣1.
(1)求抛物线C的方程;
(2)直线AF与C交于另一点B,抛物线C分别在点A,B处的切线交于点P,D为y轴正半轴上一点,直线AD与C交于另一点E,且有|FA|=|FD|,N是线段AE的靠近点A的四等分点.
(i)证明点P在△NAB的外接圆上;
(ii)△NAB的外接圆周长是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com