【题目】设复平面上点Z1 ， Z2 ， …，Zn ， …分别对应复数z1 ， z2 ， …，zn ， …；
（1）设z=r（cosα+isinα），（r＞0，α∈R），用数学归纳法证明：zn=rn（cosnα+isinnα），n∈Z+
（2）已知 ，且 （cosα+isinα）（α为实常数），求出数列{zn}的通项公式；
（3）在（2）的条件下，求 |+…．

【题目】已知复数z=bi（b∈R）， 是实数，i是虚数单位．
（1）求复数z；
（2）若复数（m+z）2所表示的点在第一象限，求实数m的取值范围．

【题目】阅读材料：根据两角和与差的正弦公式，有： sin（α+β）=sinαcosβ+cosαsinβ﹣﹣﹣﹣﹣﹣①
sin（α﹣β）=sinαcosβ﹣cosαsinβ﹣﹣﹣﹣﹣﹣②
由①+②得sin（α+β）+sin（α﹣β）=2sinαcosβ﹣﹣﹣﹣﹣﹣③
令α+β=A，α﹣β=β　有α= ，β= 代入③得　sinA+sinB=2sin cos ．
（1）利用上述结论，试求sin15°+sin75°的值；
（2）类比上述推证方法，根据两角和与差的余弦公式，证明：cosA﹣cosB=﹣2sin cos ．

【题目】阅读如图所示的程序框图，则该算法的功能是（ ）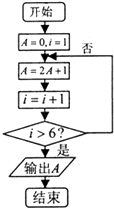

A.计算数列{2n﹣1}前5项的和
B.计算数列{2n﹣1}前5项的和
C.计算数列{2n﹣1}前6项的和
D.计算数列{2n﹣1}前6项的和

【题目】定义某种运算S=ab，运算原理如图所示，则式子[（2tan ）lg ]+[lne（ ）﹣1]的值为（ ）
A.4
B.8
C.10
D.13

【题目】我国古代数学名著《九章算术》的论割圆术中有：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣．”它体现了一种无限与有限的转化过程．比如在表达式1+ 中“…”即代表无数次重复，但原式却是个定值，它可以通过方程1+ =x求得x= ．类比上述过程，则 =（ ）
A.3
B.
C.6
D.2

【题目】执行如图所示的程序框图，若输出的S的值为64，则判断框内可填入的条件是（ ）
A.k≤3？
B.k＜3？
C.k≤4？
D.k＞4？

【题目】《聊斋志异》中有这样一首诗：“挑水砍柴不堪苦，请归但求穿墙术．得诀自诩无所阻，额上坟起终不悟．”在这里，我们称形如以下形式的等式具有“穿墙术”： 2 = ，3 = ，4 = ，5 =
则按照以上规律，若8 = 具有“穿墙术”，则n=（ ）
A.7
B.35
C.48
D.63

【题目】如图，在四棱柱ABCD﹣A1B1C1D1中，AB∥CD，AB1⊥BC，且AA1=AB．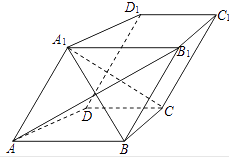

（1）求证：AB∥平面D1DCC1；
（2）求证：AB1⊥平面A1BC．

【题目】已知向量 =（cosα，﹣1）， =（2，sinα），其中 ，且 ．
（1）求cos2α的值；
（2）若sin（α﹣β）= ，且 ，求角β．