
科目: 来源: 题型:
【题目】【选修4-4:坐标系与参数方程】
极坐标系的极点为直角坐标系![]() 的原点,极轴为
的原点,极轴为![]() 轴的正半轴,两神坐标系中的长度单位相同.已知曲线
轴的正半轴,两神坐标系中的长度单位相同.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
, ![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)在曲线![]() 上求一点,使它到直线
上求一点,使它到直线![]() :
: 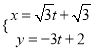 (
(![]() 为参数)的距离最短,写出
为参数)的距离最短,写出![]() 点的直角坐标.
点的直角坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】某县政府为了引导居民合理用水,决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价:若用水量不超过12吨时,按4元/吨计算水费;若用水量超过12吨且不超过14吨时,超过12吨部分按6.60元/吨计算水费;若用水量超过14吨时,超过14吨部分按7.80元/吨计算水费.为了了解全市居民月用水量的分布情况,通过抽样,获得了100户居民的月用水量(单位:吨),将数据按照![]() ,
,![]() ,…,
,…,![]() 分成8组,制成了如图1所示的频率分布直方图.
分成8组,制成了如图1所示的频率分布直方图.
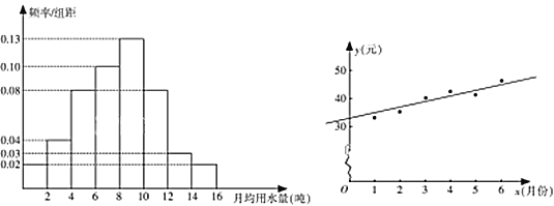
(图1) (图2)
(Ⅰ)通过频率分布直方图,估计该市居民每月的用水量的平均数和中位数(精确到0.01);
(Ⅱ)求用户用水费用![]() (元)关于月用水量
(元)关于月用水量![]() (吨)的函数关系式;
(吨)的函数关系式;
(Ⅲ)如图2是该县居民李某2017年1~6月份的月用水费![]() (元)与月份
(元)与月份![]() 的散点图,其拟合的线性回归方程是
的散点图,其拟合的线性回归方程是![]() .若李某2017年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
.若李某2017年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知向量a=(2x-y+1,x+y-2),b=(2,-2).
①当x、y为何值时,a与b共线?
②是否存在实数x、y,使得a⊥b,且|a|=|b|?若存在,求出xy的值;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 是周期为4的偶函数,当
是周期为4的偶函数,当![]() 时,
时, ![]() ,则不等式
,则不等式![]() 在区间
在区间![]() 上的解集为( )
上的解集为( )
A. (1,3) B. (-1,1) C. (-1,0)∪(1,3) D. (-1,0)∪(0,1)
查看答案和解析>>
科目: 来源: 题型:
【题目】某项运动组委会为了搞好接待工作,招募了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10人和6人喜爱运动,其余人不喜爱运动.得到下表:
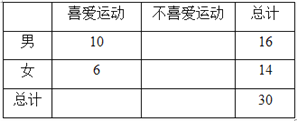
(1)根据以上数据完成2×2列联表, 问:能否在犯错误的概率不超过0.10的前提下,认为性别与喜爱运动有关?并说明理由.
(2)如果从喜欢运动的女志愿者中(其中恰有4人会外语)抽取2名,求抽出的志愿者中能胜任翻译工作的人数![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式: 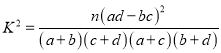
参考数据:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com