
科目: 来源: 题型:
【题目】有甲、乙两个桔柚(球形水果)种植基地,已知所有采摘的桔柚的直径都在![]() 范围内(单位:毫米,以下同),按规定直径在
范围内(单位:毫米,以下同),按规定直径在![]() 内为优质品,现从甲、乙两基地所采摘的桔柚中各随机抽取500个,测量这些桔柚的直径,所得数据整理如下:
内为优质品,现从甲、乙两基地所采摘的桔柚中各随机抽取500个,测量这些桔柚的直径,所得数据整理如下:

(1)根据以上统计数据完成下面![]() 列联表,并回答是否有
列联表,并回答是否有![]() 以上的把握认为
以上的把握认为
“桔柚直径与所在基地有关”?

(2)求优质品率较高的基地的500个桔柚直径的样本平均数![]() (同一组数据用该区间的中点值作代表):
(同一组数据用该区间的中点值作代表):
(3)经计算,甲基地的500个桔柚直径的样本方差![]() ,乙基地的500个桔柚直径的样本方差
,乙基地的500个桔柚直径的样本方差![]() ,,并且可认为优质品率较高的基地采摘的桔柚直径
,,并且可认为优质品率较高的基地采摘的桔柚直径![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .由优质品率较高的种植基地的抽样数据,估计该基地采摘的桔柚中,直径不低于86.78亳米的桔柚在总体中所占的比例.
.由优质品率较高的种植基地的抽样数据,估计该基地采摘的桔柚中,直径不低于86.78亳米的桔柚在总体中所占的比例.
附:![]() ,
,![]() .
.

若![]() ,则
,则![]() .
.
![]() ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限接近圆的面积,并创立了“割圆术”,利用“割圆术”,刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”,利用刘徽的“割圆术”思想设计的一个程序框图,则输出的值为( )
(参考数据: ![]() )
)
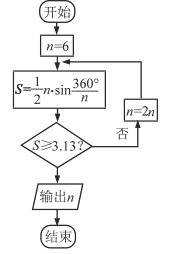
A. 12 B. 24 C. 48 D. 96
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的方程是
的方程是![]() ,圆
,圆![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)分别求直线![]() 与圆
与圆![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() :
: ![]() (
(![]() )与圆
)与圆![]() 的交点为
的交点为![]() ,
, ![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() ,射线
,射线![]() :
: ![]() 与圆
与圆![]() 交于
交于![]() ,
, ![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆系方程![]() :
: ![]() (
(![]() ,
, ![]() ),
), ![]() 是椭圆
是椭圆![]() 的焦点,
的焦点, ![]() 是椭圆
是椭圆![]() 上一点,且
上一点,且![]() .
.
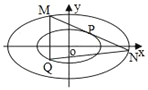
(1)求![]() 的离心率并求出
的离心率并求出![]() 的方程;
的方程;
(2)![]() 为椭圆
为椭圆![]() 上任意一点,过
上任意一点,过![]() 且与椭圆
且与椭圆![]() 相切的直线
相切的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,点
两点,点![]() 关于原点的对称点为
关于原点的对称点为![]() ,求证:
,求证: ![]() 的面积为定值,并求出这个定值.
的面积为定值,并求出这个定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】微信是当前主要的社交应用之一,有着几亿用户,覆盖范围广,及时快捷,作为移动支付的重要形式,微信支付成为人们支付的重要方式和手段。某公司为了解人们对“微信支付”认可度,对![]() 年龄段的人群随机抽取
年龄段的人群随机抽取![]() 人进行了一次“你是否喜欢微信支付”的问卷调查,根据调查结果得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次“你是否喜欢微信支付”的问卷调查,根据调查结果得到如下统计表和各年龄段人数频率分布直方图:
组号 | 分组 | 喜欢微信支付的人数 | 喜欢微信支付的人数 占本组的频率 |
第一组 |
|
|
|
第二组 |
|
|
|
第三组 |
|
|
|
第四组 |
|
|
|
第五组 |
|
|
|
第六组 |
|
|
|

(1)补全频率分布直方图,并求![]() ,
, ![]() ,
, ![]() 的值;
的值;
(2)在第四、五、六组“喜欢微信支付”的人中,用分层抽样的方法抽取![]() 人参加“微信支付日鼓励金”活动,求第四、五、六组应分别抽取的人数;
人参加“微信支付日鼓励金”活动,求第四、五、六组应分别抽取的人数;
(3)在(2)中抽取的![]() 人中随机选派
人中随机选派![]() 人做采访嘉宾,求所选派的
人做采访嘉宾,求所选派的![]() 人没有第四组人的概率.
人没有第四组人的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com