
科目: 来源: 题型:
【题目】在平面直角坐标系内,已知点![]() 及线段
及线段![]() ,在线段
,在线段![]() 上任取一点
上任取一点![]() ,线段
,线段![]() 长度的最小值称为“点
长度的最小值称为“点![]() 到线段
到线段![]() 的距离”,记为
的距离”,记为![]() .
.
(1)设点![]() ,线段
,线段![]()
![]() ,求
,求![]() ;
;
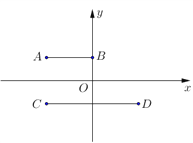
(2)设![]() ,
, ![]() ,
, ![]() ,
, ![]() ,线段
,线段![]() ,线段
,线段![]() ,若点
,若点![]() 满足
满足![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出该函数的值域.
的函数解析式,并写出该函数的值域.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,设倾斜角为
中,设倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数)与曲线
为参数)与曲线 (
(![]() 为参数)相交于不同的两点
为参数)相交于不同的两点![]() 、
、![]() .
.
(1)若![]() ,求线段
,求线段![]() 的中点的直角坐标;
的中点的直角坐标;
(2)若直线![]() 的斜率为
的斜率为![]() ,且过已知点
,且过已知点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,
, ![]() 、
、![]() 为椭圆的左右顶点,焦点到短轴端点的距离为2,
为椭圆的左右顶点,焦点到短轴端点的距离为2, ![]() 、
、![]() 为椭圆
为椭圆![]() 上异于
上异于![]() 、
、![]() 的两点,且直线
的两点,且直线![]() 的斜率等于直线
的斜率等于直线![]() 斜率的2倍.
斜率的2倍.

(Ⅰ)求证:直线![]() 与直线
与直线![]() 的斜率乘积为定值;
的斜率乘积为定值;
(Ⅱ)求三角形![]() 的面积
的面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,多面体![]() 中,四边形
中,四边形![]() 是菱形,
是菱形, ![]() ,
, ![]() 相交于
相交于![]() ,
, ![]() ,点
,点![]() 在平面
在平面![]() 上的射影恰好是线段
上的射影恰好是线段![]() 的中点.
的中点.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)若直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成角(锐角)的余弦值.
所成角(锐角)的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4吨,硝酸盐18吨;生产1车皮乙种肥料需要的主要原料是磷酸盐1吨,硝酸盐15吨.现库存磷酸盐10吨,硝酸盐66吨,在此基础上生产这两种混合肥料.如果生产1车皮甲种肥料产生的利润为12 000元,生产1车皮乙种肥料产生的利润为7 000元,那么可产生的最大利润是( )
A. 29 000元 B. 31 000元 C. 38 000元 D. 45 000元
查看答案和解析>>
科目: 来源: 题型:
【题目】现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥P—A1B1C1D1,下部的形状是正四棱柱ABCD—A1B1C1D1(如图所示),并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍.
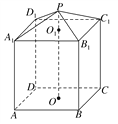
(1)若AB=6 m,PO1=2 m,则仓库的容积是多少?
(2)若正四棱锥的侧棱长为6 m,则当PO1为多少时,仓库的容积最大?
查看答案和解析>>
科目: 来源: 题型:
【题目】“扶贫帮困”是中华民族的传统美德,某校为帮扶困难同学,采用如下方式进行一次募捐:在不透明的箱子中放入大小均相同的白球七个,红球三个,每位献爱心的参与者投币20元有一次摸奖机会,一次性从箱子中摸球三个(摸完球后将球放回),若有一个红球,奖金10元,两个红球奖金20元,三个全是红球奖金100元.
(1)求献爱心参与者中将的概率;
(2)若该次募捐900位献爱心参与者,求此次募捐所得善款的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com