
科目: 来源: 题型:
【题目】如图,在等腰梯形![]() 中,
中, ![]() ,上底
,上底![]() ,下底
,下底![]() ,点
,点![]() 为下底
为下底![]() 的中点,现将该梯形中的三角形
的中点,现将该梯形中的三角形![]() 沿线段
沿线段![]() 折起,形成四棱锥
折起,形成四棱锥![]() .
.

(1)在四棱锥![]() 中,求证:
中,求证: ![]() ;
;
(2)若平面![]() 与平面
与平面![]() 所成二面角的平面角为
所成二面角的平面角为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,飞镖的标靶呈圆盘形,圆盘被10等分,按如图所示染色为Ⅰ、Ⅱ、Ⅲ三部分,某人依次将若干支飞镖投向标靶,如果每次投射都是相互独立的.
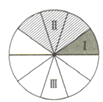
(1)如果他投向标靶的飞镖恰有2支且都击中标靶,同时每支飞镖击中标靶的任意位置都是等可能的,求“第Ⅰ部分被击中2次或第Ⅱ部分被击中2次”的概率;
(2)如果他投向标靶的飞镖恰有4支,且他投射1支飞镖,击中标靶的概率为![]() ,设
,设![]() 表示标靶被击中的次数,求
表示标靶被击中的次数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】有甲乙两家公司都愿意聘用某求职者,这两家公式的具体聘用信息如下:

(1)根据以上信息,如果你是该求职者,你会选择哪一家公司?说明理由;
(2)某课外实习作业小组调查了1000名职场人士,就选择这两家公司的意愿作了统计,得到如下数据分布:

若分析选择意愿与年龄这两个分类变量,计算得到的![]() 的观测值为
的观测值为![]() ,测得出“选择意愿与年龄有关系”的结论犯错误的概率的上限是多少?并用统计学知识分析,选择意愿与年龄变量和性别变量哪一个关联性更大?
,测得出“选择意愿与年龄有关系”的结论犯错误的概率的上限是多少?并用统计学知识分析,选择意愿与年龄变量和性别变量哪一个关联性更大?
附: 
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的右顶点与抛物线
的右顶点与抛物线![]() 的焦点重合,椭圆
的焦点重合,椭圆![]() 的离心率为
的离心率为![]() ,过椭圆
,过椭圆![]() 的右焦点
的右焦点![]() 且垂直于
且垂直于![]() 轴的直线截抛物线所得的弦长为.
轴的直线截抛物线所得的弦长为.
(1)求椭圆![]() 和抛物线
和抛物线![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,证明:直线
,证明:直线![]() 恒过一定点.
恒过一定点.
查看答案和解析>>
科目: 来源: 题型:
【题目】某课外实习作业小组调查了1000名职场人士,就入职两家公司的意愿做了统计,得到如下数据分布:
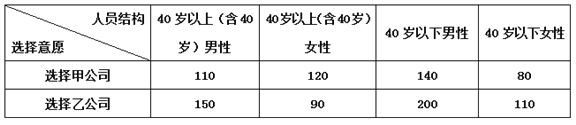
(1)请分别计算40岁以上(含40岁)与40岁以下全体中选择甲公司的频率(保留两位小数),根据计算结果,你能初步得出什么结论?
(2)若分析选择意愿与年龄这两个分类变量,计算得到的![]() 的观测值为
的观测值为![]() ,测得出“选择意愿与年龄有关系”的结论犯错误的概率的上限是多少?并用统计学知识分析,选择意愿与年龄变量和性别变量哪一个关联性更大?
,测得出“选择意愿与年龄有关系”的结论犯错误的概率的上限是多少?并用统计学知识分析,选择意愿与年龄变量和性别变量哪一个关联性更大?
附: 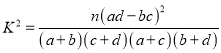

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com