【题目】已知椭圆E： （a﹥b﹥0）的一个焦点与短轴的两个端点是正三角形的三个顶点，点在椭圆E上.

（Ⅰ）求椭圆E的方程；

（Ⅱ）设不过原点O且斜率为的直线l与椭圆E交于不同的两点A，B，线段AB的中点为M，直线OM与椭圆E交于C，D，证明：|MA|·|MB|=|MC|·|MD|.

【题目】如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80 m.经测量，点A位于点O正北方向60 m处,点C位于点O正东方向170 m处(OC为河岸),tan∠BCO=.

（1）求新桥BC的长;

（2）当OM多长时,圆形保护区的面积最大?

(1)求；

(2)除H以外，直线MH与C是否有其它公共点？说明理由．

【题目】在直角坐标系xOy中，曲线C1： (t为参数，t≠0)，其中0≤α＜π.在以O为极点，x轴正半轴为极轴的极坐标系中，曲线C2：ρ＝2sin θ，C3：ρ＝2cos θ.

(1)求C2与C3交点的直角坐标；

(2)若C1与C2相交于点A，C1与C3相交于点B，求|AB|的最大值．

(1)当过点A的圆C的切线存在时，求实数a的取值范围；

(2)设AM、AN为圆C的两条切线，M、N为切点，当MN＝时，求MN所在直线的方程．

【题目】如图所示，射线OA、OB分别与x轴正半轴成45°和30°角，过点P(1,0)作直线AB分别交OA、OB于A、B两点，当AB的中点C恰好落在直线y＝x上时，求直线AB的方程．

【题目】已知函数f(x)的导函数f′(x)，且对任意x＞0，都有f′(x)＞.

(1)判断函数F(x)＝在(0，＋∞)上的单调性；

(2)设x1，x2∈(0，＋∞)，证明：f(x1)＋f(x2)＜f(x1＋x2)；

(3)请将(2)中结论推广到一般形式，并证明你所推广的结论．

(1)若平面ABCD⊥平面DCEF，求直线MN与平面DCEF所成角的正弦值；

(2)用反证法证明：直线ME与BN是两条异面直线．

【题目】为了净化空气，某科研单位根据实验得出，在一定范围内，每喷洒1个单位的净化剂，空气中释放的浓度y(单位：毫克/立方米)随着时间x(单位：天)变化的函数关系式近似为y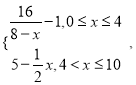＝ 若多次喷洒，则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和．由实验知，当空气中净化剂的浓度不低于4(毫克/立方米)时，它才能起到净化空气的作用．

(1)若一次喷洒4个单位的净化剂，则净化时间可达几天？

(2)若第一次喷洒2个单位的净化剂，6天后再喷洒a(1≤a≤4)个单位的药剂，要使接下来的4天中能够持续有效净化，试求a的最小值(精确到0.1，参考数据: 取1.4)．

（1）求数列{an}的通项公式；

（2）数列{nan}的前n项和为Tn，若对任意正整数n，都有Tn∈[a，b]，求b－a的最小值．