
科目: 来源: 题型:
【题目】给出下面四个类比结论:
①实数a,b,若ab=0,则a=0或b=0;类比复数z1,z2,若z1z2=0,则z1=0或z2=0.
②实数a,b,若ab=0,则a=0或b=0;类比向量a,b,若a·b=0,则a=0或b=0.
③实数a,b,有a2+b2=0,则a=b=0;类比复数z1,z2,有z+z=0,则z1=z2=0.
④实数a,b,有a2+b2=0,则a=b=0;类比向量a,b,若a2+b2=0,则a=b=0.
其中类比结论正确的个数是( )
A. 0 B. 1
C. 2 D. 3
查看答案和解析>>
科目: 来源: 题型:
【题目】(2017·郑州第二次质量预测)如图,高为1的等腰梯形ABCD中,AM=CD=![]() AB=1.现将△AMD沿MD折起,使平面AMD⊥平面MBCD,连接AB,AC.
AB=1.现将△AMD沿MD折起,使平面AMD⊥平面MBCD,连接AB,AC.
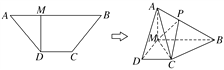
(1)在AB边上是否存在点P,使AD∥平面MPC?
(2)当点P为AB边的中点时,求点B到平面MPC的距离.
查看答案和解析>>
科目: 来源: 题型:
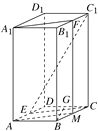
【题目】(2017·泰安模拟)如图,在正四棱柱ABCDA1B1C1D1中,E为AD的中点,F为B1C1的中点.
(1)求证:A1F∥平面ECC1;
(2)在CD上是否存在一点G,使BG⊥平面ECC1?若存在,请确定点G的位置,并证明你的结论,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】(2017·北京高考)由四棱柱ABCDA1B1C1D1截去三棱锥C1B1CD1后得到的几何体如图所示.四边形ABCD为正方形,O为AC与BD的交点,E为AD的中点,A1E⊥平面ABCD.
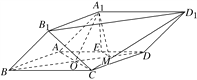
(1)证明:A1O∥平面B1CD1;
(2)设M是OD的中点,证明:平面A1EM⊥平面B1CD1.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥PABCD中,AB∥CD ,且∠BAP=∠CDP =90°.
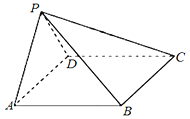
(1).证明:平面PAB⊥平面PAD;
(2).若PA=PD=AB=DC, ∠APD =90°,且四棱锥PABCD的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
查看答案和解析>>
科目: 来源: 题型:
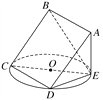
【题目】(2017·安徽名校阶段性测试)如图所示,正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦,AE垂直于圆O所在平面,垂足E是圆O上异于C,D的点,AE=3,圆O的直径CE=9.
(1)求证:平面ABE⊥平面ADE;
(2)求五面体ABCDE的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AD=CD=![]() AB=2,将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体DABC.
AB=2,将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体DABC.
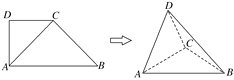
(1)求证:AD⊥平面BCD;
(2)求三棱锥CABD的高.
查看答案和解析>>
科目: 来源: 题型:
【题目】(2017·江苏高考)如图,在三棱锥ABCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E,F(E与A,D不重合)分别在棱AD,BD上,且EF⊥AD.

求证:(1)EF∥平面ABC;
(2)AD⊥AC.
查看答案和解析>>
科目: 来源: 题型:
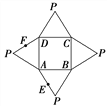
【题目】如图是一几何体的平面展开图,其中ABCD为正方形,E,F分别为PA,PD的中点,
在此几何体中,给出下面四个结论:
①直线BE与直线CF异面; ②直线BE与直线AF异面;
③直线EF∥平面PBC; ④平面BCE⊥平面PAD.
其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在三棱锥PABC中,不能证明AP⊥BC的条件是( )
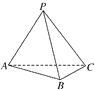
A. AP⊥PB,AP⊥PC
B. AP⊥PB,BC⊥PB
C. 平面BPC⊥平面APC,BC⊥PC
D. AP⊥平面PBC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com