
科目: 来源: 题型:
【题目】如图,已知四棱锥P—ABCD,底面ABCD是边长为4的菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
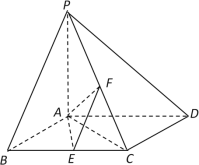
(Ⅰ)求证:AE⊥PD;
(Ⅱ)若PA=4,求二面角E—AF—C的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还须从物理,化学,生物,历史,地理和政治六个科目中选取三个科目作为选考科目.若一个学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定.例如,学生甲选择“物理、化学和生物”三个选考科目,则学生甲的选考方案确定,“物理、化学和生物”为其选考方案.
某学校为了解高一年级420名学生选考科目的意向,随机选取30名学生进行了一次调查,统计选考科目人数如下表:
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 |
男生 | 选考方案确定的有8人 | 8 | 8 | 4 | 2 | 1 | 1 |
选考方案待确定的有6人 | 4 | 3 | 0 | 1 | 0 | 0 | |
女生 | 选考方案确定的有10人 | 8 | 9 | 6 | 3 | 3 | 1 |
选考方案待确定的有6人 | 5 | 4 | 1 | 0 | 0 | 1 |
(Ⅰ)估计该学校高一年级选考方案确定的学生中选考生物的学生有多少人?
(Ⅱ)假设男生、女生选择选考科目是相互独立的.从选考方案确定的8位男生中随机选出1人,从选考方案确定的10位女生中随机选出1人,试求该男生和该女生的选考方案中都含有历史学科的概率;
(Ⅲ)从选考方案确定的8名男生中随机选出2名,设随机变量![]() ,求
,求![]() .
.
查看答案和解析>>
科目: 来源: 题型:
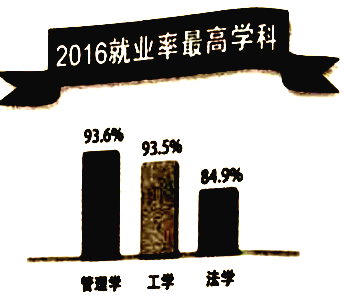
【题目】某网站调查2016年大学毕业生就业状况,其中一项数据显示“2016年就业率最高学科”为管理学,高达![]() (数据来源于网络,仅供参考).为了解高三学生对“管理学”的兴趣程度,某校学生社团在高校高三文科班进行了问卷调查,问卷共100道选择题,每题1分,总分100分,社团随机抽取了100名学生的问卷成绩(单位:分)进行统计,得到频率分布表如下:
(数据来源于网络,仅供参考).为了解高三学生对“管理学”的兴趣程度,某校学生社团在高校高三文科班进行了问卷调查,问卷共100道选择题,每题1分,总分100分,社团随机抽取了100名学生的问卷成绩(单位:分)进行统计,得到频率分布表如下:
组号 | 分组 | 男生 | 女生 | 频数 | 频率 |
第一组 |
| 3 | 2 | 5 | 0.05 |
第二组 |
| 17 |
|
|
|
第三组 |
| 20 | 10 | 30 | 0.3 |
第四组 |
| 6 | 18 | 24 | 0.24 |
第五组 |
| 4 | 12 | 16 | 0.16 |
合计 | 50 | 50 | 100 | 1 | |
(1)求频率分布表中![]() ,
, ![]() ,
, ![]() 的值;
的值;
(2)若将得分不低于60分的称为“管理学意向”学生,将低于60分的称为“非管理学意向”学生,根据条件完成下面![]() 列联表,并据此判断是否有
列联表,并据此判断是否有![]() 的把握认为是否为“管理学意向”与性别有关?
的把握认为是否为“管理学意向”与性别有关?
非管理学意向 | 管理学意向 | 合计 | |
男生 |
|
| |
女生 |
|
| |
合计 |
(3)心理咨询师认为得分低于20分的学生可能“选择困难”,要从“选择困难”的5名学生中随机抽取2名学生进行心理辅导,求恰好有1名男生,1名女生被选中的概率.
参考公式: 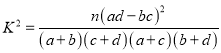 ,其中
,其中![]() .
.
参考临界值:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在多边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是线段
是线段![]() 上的一点,且
上的一点,且![]() ,若将
,若将![]() 沿
沿![]() 折起,得到几何体
折起,得到几何体![]() .
.
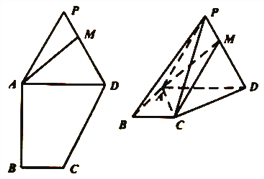
(1)试问:直线![]() 与平面
与平面![]() 是否有公共点?并说明理由;
是否有公共点?并说明理由;
(2)若![]() ,且平面
,且平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市举行“中学生诗词大赛”,分初赛和复赛两个阶段进行,规定:初赛成绩大于90分的具有复赛资格.某校有800 名学生参加了初赛,所有学生的成绩均在区间![]() 内,其频率分布直方图如图所示.
内,其频率分布直方图如图所示.
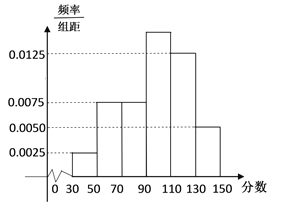
(Ⅰ)求初赛分数在区间![]() 内的频率;
内的频率;
(Ⅱ)求获得复赛资格的人数;
(Ⅲ)据此直方图估算学生初赛成绩的平均数.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解市民对A,B两个品牌共享单车使用情况的满意程度,分别从使用A,B两个品牌单车的市民中随机抽取了100人,对这两个品牌的单车进行评分,满分60分.根据调查,得到A品牌单车评分的频率分布直方图,和B品牌单车评分的频数分布表:


根据用户的评分,定义用户对共享单车评价的“满意度指数”如下:
评分 |
|
|
|
满意度指数 |
|
|
|
(1)求对A品牌单车评价“满意度指数”为![]() 的人数;
的人数;
(2)从对A,B两个品牌单车评分都在![]() 范围内的人中随机选出2人,求2人中恰有1人是A品牌单车的评分人的概率;
范围内的人中随机选出2人,求2人中恰有1人是A品牌单车的评分人的概率;
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (限定
(限定![]() ).
).
(1)写出曲线![]() 的极坐标方程,并求
的极坐标方程,并求![]() 与
与![]() 交点的极坐标;
交点的极坐标;
(2)射线![]() 与曲线
与曲线![]() 与
与![]() 分别交于点
分别交于点![]() (
(![]() 异于原点),求
异于原点),求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数f(x)=|x+2|+|x-2|,x∈R,不等式f(x)≤6的解集为M.
(1)求M;
(2)当a2,b2∈M时,证明: ![]() |a+b|≤|ab+3|.
|a+b|≤|ab+3|.
查看答案和解析>>
科目: 来源: 题型:
【题目】下面有五个命题:
①函数![]() 的最小正周期是
的最小正周期是![]() ;
;
②终边在y轴上的角的集合是![]() ;
;
③在同一坐标系中,函数![]() 的图象和函数
的图象和函数![]() 的图象有一个公共点;
的图象有一个公共点;
④把函数![]() ;
;
⑤在![]() 中,若
中,若![]() ,则
,则![]() 是等腰三角形
是等腰三角形![]() ;
;
其中真命题的序号是( )
A.(1)(2)(3) B.(2)(3)(4)
C.(3)(4)(5) D.(1)(4)(5)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com