
科目: 来源: 题型:
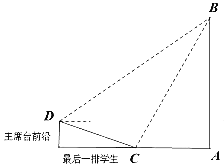
【题目】如图,学校升旗仪式上,主持人站在主席台前沿D处,测得旗杆AB顶部的仰角为![]() 俯角最后一排学生C的俯角为
俯角最后一排学生C的俯角为![]() 最后一排学生C测得旗杆顶部的仰角为
最后一排学生C测得旗杆顶部的仰角为![]() 旗杆底部与学生在一个水平面上,并且不计学生身高.
旗杆底部与学生在一个水平面上,并且不计学生身高.
(1)设![]() 米,试用
米,试用![]() 和
和![]() 表示旗杆的高度AB(米);
表示旗杆的高度AB(米);
(2)测得![]() 米,
米,![]() 若国歌长度约为50秒,国旗班升旗手应以多大的速度匀速升旗才能是国旗到达旗杆顶点时师生的目光刚好停留在B处?
若国歌长度约为50秒,国旗班升旗手应以多大的速度匀速升旗才能是国旗到达旗杆顶点时师生的目光刚好停留在B处?
查看答案和解析>>
科目: 来源: 题型:
【题目】如下图,过抛物线![]() 上一定点
上一定点![]() ,作两条直线分别交抛物线于
,作两条直线分别交抛物线于![]() ,
,![]() .
.

(1)求该抛物线上纵坐标为![]() 的点到其焦点
的点到其焦点![]() 的距离;
的距离;
(2)当![]() 与
与![]() 的斜率存在且倾斜角互补时,求
的斜率存在且倾斜角互补时,求![]() 的值,并证明直线
的值,并证明直线![]() 的斜率是非零常数.
的斜率是非零常数.
查看答案和解析>>
科目: 来源: 题型:
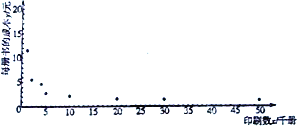
【题目】为研究某种图书每册的成本费![]() (元)与印刷数
(元)与印刷数![]() (千册)的关系,收集了一些数据并作了初步处理,得到了下面的散点图及一些统计量的值.
(千册)的关系,收集了一些数据并作了初步处理,得到了下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
15.25 | 3.63 | 0.269 | 2085.5 |
| 0.787 | 7.049 |
表中![]() ,
, ![]() .
.
(1)根据散点图判断: ![]() 与
与![]() 哪一个更适宜作为每册成本费
哪一个更适宜作为每册成本费![]() (元)与印刷数
(元)与印刷数![]() (千册)的回归方程类型?(只要求给出判断,不必说明理由)
(千册)的回归方程类型?(只要求给出判断,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程(回归系数的结果精确到0.01);
的回归方程(回归系数的结果精确到0.01);
(3)若每册书定价为10元,则至少应该印刷多少册才能使销售利润不低于78840元?(假设能够全部售出,结果精确到1)
(附:对于一组数据![]() ,
, ![]() ,…,
,…, ![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为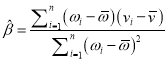 ,
, ![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 中点(如图1).将
中点(如图1).将![]() 沿
沿![]() 折起到图2中
折起到图2中![]() 的位置,得到四棱锥
的位置,得到四棱锥![]() .
.

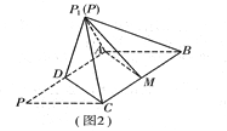
(1)将![]() 沿
沿![]() 折起的过程中,
折起的过程中, ![]() 平面
平面![]() 是否成立?并证明你的结论;
是否成立?并证明你的结论;
(2)若![]() ,过
,过![]() 的平面交
的平面交![]() 于点
于点![]() ,且
,且![]() 为
为![]() 的中点,求三棱锥
的中点,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】“干支纪年法”是中国历法上自古以来使用的纪年方法,甲、乙、丙、丁、戊、己、庚、辛、壬、癸被称为“十天干”,子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥叫做“十二地支”。“天干”以“甲”字开始,“地支”以“子”字开始,两者按干支顺序相配,组成了干支纪年法,其相配顺序为:甲子、乙丑、丙寅…癸酉,甲戌、乙亥、丙子…癸末,甲申、乙酉、丙戌…癸巳,…,共得到![]() 个组成,周而复始,循环记录。2014年是“干支纪年法”中的甲午年,那么2020年是“干支纪年法”中的()
个组成,周而复始,循环记录。2014年是“干支纪年法”中的甲午年,那么2020年是“干支纪年法”中的()
A. 己亥年 B. 戊戌年 C. 辛丑年 D. 庚子年
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() :
:![]() ,焦点为
,焦点为![]() ,其准线与
,其准线与![]() 轴交于点
轴交于点![]() .椭圆
.椭圆![]() :分别以
:分别以![]() 、
、![]() 为左、右焦点,其离心率
为左、右焦点,其离心率![]() ,且抛物线
,且抛物线![]() 和椭圆
和椭圆![]() 的一个交点记为
的一个交点记为![]() .
.
(1)当![]() 时,求椭圆
时,求椭圆![]() 的标准方程;
的标准方程;
(2)在(1)的条件下,若直线![]() 经过椭圆
经过椭圆![]() 的右焦点
的右焦点![]() ,且与抛物线
,且与抛物线![]() 相交于
相交于![]() ,
,![]() 两点,若弦长
两点,若弦长![]() 等于
等于![]() 的周长,求直线
的周长,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是2017年第一季度中国某五省![]() 情况图,则下列陈述正确的是( )
情况图,则下列陈述正确的是( )
①2017年第一季度 ![]() 总量高于4000亿元的省份共有3个;
总量高于4000亿元的省份共有3个;
②与去年同期相比,2017年第一季度五个省的![]() 总量均实现了增长;
总量均实现了增长;
③去年同期的![]() 总量前三位依次是
总量前三位依次是![]() 省、
省、![]() 省、
省、![]() 省;
省;
④2016年同期![]() 省的
省的![]() 总量居于第四位.
总量居于第四位.
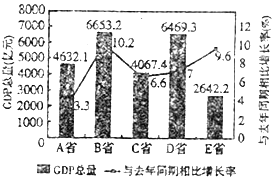
A. ①② B. ②③④ C. ②④ D. ①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com