
【题目】如下图,过抛物线![]() 上一定点
上一定点![]() ,作两条直线分别交抛物线于
,作两条直线分别交抛物线于![]() ,
,![]() .
.

(1)求该抛物线上纵坐标为![]() 的点到其焦点
的点到其焦点![]() 的距离;
的距离;
(2)当![]() 与
与![]() 的斜率存在且倾斜角互补时,求
的斜率存在且倾斜角互补时,求![]() 的值,并证明直线
的值,并证明直线![]() 的斜率是非零常数.
的斜率是非零常数.
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足条件f(0)=1,及f(x+1)﹣f(x)=2x.
(1)求函数f(x)的解析式;
(2)在区间[﹣1,1]上,y=f(x)的图象恒在y=2x+m的图象上方,试确定实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 中点(如图1).将
中点(如图1).将![]() 沿
沿![]() 折起到图2中
折起到图2中![]() 的位置,得到四棱锥
的位置,得到四棱锥![]() .
.

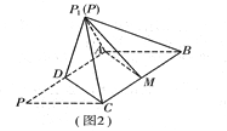
(1)将![]() 沿
沿![]() 折起的过程中,
折起的过程中, ![]() 平面
平面![]() 是否成立?并证明你的结论;
是否成立?并证明你的结论;
(2)若![]() ,过
,过![]() 的平面交
的平面交![]() 于点
于点![]() ,且
,且![]() 为
为![]() 的中点,求三棱锥
的中点,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分) 已知双曲线![]() 的两个焦点为
的两个焦点为![]() 的曲线C上.
的曲线C上.
(Ⅰ)求双曲线C的方程;
(Ⅱ)记O为坐标原点,过点Q(0,2)的直线l与双曲线C相交于不同的两点E、F,若△OEF的面积为![]() 求直线l的方程
求直线l的方程
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4吨、硝酸盐18吨;生产1车皮乙种肥料的主要原料是磷酸盐1吨、硝酸盐15吨,现库存磷酸盐10吨、硝酸盐66吨,在此基础上生产这两种混合肥料。如果生产1车皮甲种肥料,产生的利润为12000元;生产1车皮乙种肥料,产生的利润为7000元。那么可产生最大的利润是__________元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们国家正处于老龄化社会中,老有所依也是政府的民生工程.某市有户籍的人口共![]() 万,其中老人(年龄
万,其中老人(年龄![]() 岁及以上)人数约有
岁及以上)人数约有![]() 万,为了了解老人们的健康状况,政府从老人中随机抽取
万,为了了解老人们的健康状况,政府从老人中随机抽取![]() 人并委托医疗机构免费为他们进行健康评估,健康状况共分为不能自理、不健康尚能自理、基本健康、健康四个等级,并以
人并委托医疗机构免费为他们进行健康评估,健康状况共分为不能自理、不健康尚能自理、基本健康、健康四个等级,并以![]() 岁为界限分成两个群体进行统计,样本分布被制作成如下图表:
岁为界限分成两个群体进行统计,样本分布被制作成如下图表:

(1)若从样本中的不能自理的老人中采取分层抽样的方法再抽取![]() 人进一步了解他们的生活状况,则两个群体中各应抽取多少人?
人进一步了解他们的生活状况,则两个群体中各应抽取多少人?
(2)估算该市![]() 岁以上长者占全市户籍人口的百分比;
岁以上长者占全市户籍人口的百分比;
(3)政府计划为![]() 岁及以上长者或生活不能自理的老人每人购买
岁及以上长者或生活不能自理的老人每人购买![]() 元/年的医疗保险,为其余老人每人购买
元/年的医疗保险,为其余老人每人购买![]() 元/年的医疗保险,不可重复享受,试估计政府执行此计划的年度预算.
元/年的医疗保险,不可重复享受,试估计政府执行此计划的年度预算.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com