【题目】已知函数．

（1）讨论函数的单调性；

（2） 若函数有两个零点， ，且，证明： ．

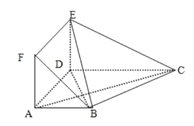
【题目】在多面体中，底面是梯形，四边形是正方形，，，面面，..

（1）求证：平面平面；

（2）设为线段上一点，，试问在线段上是否存在一点，使得平面，若存在，试指出点的位置；若不存在，说明理由?

（3）在（2）的条件下，求点到平面的距离.

（1）根据茎叶图计算样本均值；

（2）若网购金额(单位：万元)不小于18的服务站定义为优秀服务站，其余为非优秀服务站.根据茎叶图推断90间服务站中有几间优秀服务站？

（3）从随机抽取的5间服务站中再任取2间作网购商品的调查，求恰有1间是优秀服务站的概率.

【题目】某厂家拟在2020年举行促销活动，经调查测算，某产品的年销售量（即该厂的年产量）万件与年促销费用万元，满足（为常数），如果不搞促销活动，则该产品的年销售量只能是1万件，已知2020年生产该产品的固定投入为8万元，每生产1万件，该产品需要再投入16万元，厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍（产品成本包括固定投入和再投入两部分资金）.

（1）将2020年该产品的利润（万元）表示为年促销费用（万元）的函数；

（2）该厂家2020年的促销费用投入多少万元时，厂家的利润最大？

【题目】已知如下四个命题：①在线性回归模型中，相关指数表示解释变量对于预报变量的贡献率，越接近于，表示回归效果越好；②在回归直线方程中，当解释变量每增加一个单位时，预报变量平均增加个单位；③两个变量相关性越强，则相关系数的绝对值就越接近于；④对分类变量与，对它们的随机变量的观测值来说，越小，则“与有关系”的把握程度越大．其中正确命题的序号是__________．

【题目】某地区上年度电价为元/（），年用电量为．本年度该地政府实行惠民政策，要求电力部门让利给用户，将电价下调到元/（）至元/（）之间，而用户的期望电价为元/（）．经测算，下调电价后新增用电量和实际电价与用户的期望电价的差成反比（比例系数为）．该地区的电力成本价为元/（）．

（1）写出本年度电价下调后电力部门的收益（单位：元）关于实际电价（单位：元/（）的函数解析式；（收益实际用电量（实际电价成本价））

（2）设，当电价最低定为多少时，可保证电力部门的收益比上年至多减少？

【题目】已知f（x）为二次函数，且．

（1）求f（x）的表达式；

（2）判断函数在（0，+∞）上的单调性，并证明．

【题目】如图，已知直四棱柱的底面是直角梯形，，，、分别是棱、上的动点，且，，，.

（1）证明：无论点怎样运动，四边形都为矩形；

（2）当时，求几何体的体积.

【题目】在正方体中，、分别为、的中点，，，如图.

（1）若交平面于点，证明：、、三点共线；

（2）线段上是否存在点，使得平面平面，若存在确定的位置，若不存在说明理由.

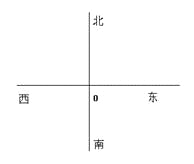
（I）若希望相遇时小艇的航行距离最小，则小艇航行速度的大小应为多少？

（II）为保证小艇在30分钟内（含30分钟）能与轮船相遇，试确定小艇航行速度的最小值．