(1)求频率分布直方图中a的值；

(2)估计总体中成绩落在[50，60)中的学生人数；

(3)根据频率分布直方图估计20名学生数学考试成绩的众数，平均数；

【题目】【2018届广东省汕头市高三上学期期末】某大型企业为鼓励员工多利用网络进行营销，准备为员工办理手机流量套餐.为了解员工手机流量使用情况，通过抽样，得到100位员工每人手机月平均使用流量 (单位: )的数据，其频率分布直方图如下：

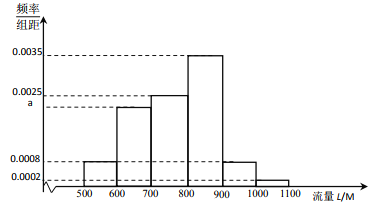
将频率视为概率，同一组中的数据用该组区间的中点值代替，回答以下问题:

(1) 求出的值，并计算这100位员工每月手机使用流量的平均值；

(2) 据了解，某网络营运商推出两款流量套餐，详情如下：

流量套餐的规则是：每月1日收取套餐费。如果手机实际使用流量超出套餐流量，则需要购买流量叠加包，每一个叠加包(包含的流量)需要10元，可以多次购买；如果当月流量有剩余，将会被清零.

该企业准备订购其中一款流量套餐，每月为员工支付套餐费，以及购买流量叠加包所需月费用.若以平均费用为决策依据，该企业订购哪一款套餐更经济？

（1）当每辆车的月租金定为3600元时，能租出多少辆车？

（2）当每辆车的月租金定为多少元时，租赁公司的月收益最大？最大月收益是多少？

在这10名学生中，进入立定跳远决赛的有8人，同时进入立定跳远决赛和30秒跳绳决赛的有6人，则（ ）

A. 2号学生进入30秒跳绳决赛 B. 5号学生进入30秒跳绳决赛

C. 8号学生进入30秒跳绳决赛 D. 9号学生进入30秒跳绳决赛

(1) 取出的两球1个是白球，另1个是红球；

(2) 取出的两球至少一个是白球。

【题目】已知F1、F2分别为双曲线的左、右焦点，若双曲线左支上存在一点P，使得=8a，则双曲线的离心率的取值范围是__________________．

已知极坐标系的极点与直角坐标系的原点重合，极轴与直角坐标系中轴的正半轴重合.若曲线的参数方程为（为参数），直线的极坐标方程为.

（1）将曲线的参数方程化为极坐标方程；

（2）由直线上一点向曲线引切线，求切线长的最小值.

A. 甲地：总体均值为3，中位数为4 B. 乙地：总体均值为1，总体方差大于0

C. 丙地：中位数为2，众数为3 D. 丁地：总体均值为2，总体方差为3

【题目】定义域为的函数满足：，且对于任意实数，恒有，当时，.

（1）求的值，并证明当时，；

（2）判断函数在上的单调性并加以证明；

（3）若不等式对任意恒成立，求实数的取值范围.

(1)求k的取值范围；

(2)若＝12，其中O为坐标原点，求|MN|.