
科目: 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]
在平面直角坐标系xOy中,直线l的参数方程为 (t为参数),以平面直角坐标系的原点为极点,正半轴为极轴,取相同的长度单位建立极坐标系,曲线C的极坐标方程为
(t为参数),以平面直角坐标系的原点为极点,正半轴为极轴,取相同的长度单位建立极坐标系,曲线C的极坐标方程为![]() .
.
(Ⅰ)求直线l和曲线C的直角坐标方程,并指明曲线C的形状;
(Ⅱ)设直线l与曲线C交于A,B两点,O为坐标原点,且|OA|<|OB|,求![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆![]() ,圆
,圆![]() 内一定点
内一定点![]() ,动圆
,动圆![]() 过点
过点![]() 且与圆
且与圆![]() 内切.记动圆圆心
内切.记动圆圆心![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求轨迹![]() 方程;
方程;
(II)过点![]() 的动直线l交轨迹
的动直线l交轨迹![]() 于M,N两点,试问:在坐标平面上是否存在一个定点Q,使得以线段MN为直径的圆恒过点Q?若存在,求出点Q的坐标;若不存在,请说明理由.
于M,N两点,试问:在坐标平面上是否存在一个定点Q,使得以线段MN为直径的圆恒过点Q?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,底面ABCD为矩形,PA=PB,O为AB的中点,OD⊥PC.

(Ⅰ) 求证:OC⊥PD;
(II)若PD与平面PAB所成的角为30°,求二面角D-PC-B的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,且过点A (2,2),椭圆
的焦点为F,且过点A (2,2),椭圆![]() 的离心率为
的离心率为![]() ,点B为抛物线C与椭圆D的一个公共点,且
,点B为抛物线C与椭圆D的一个公共点,且![]() .
.
(Ⅰ)求椭圆D的方程;
(Ⅱ)过椭圆内一点P(0,t)的直线l的斜率为k,且与椭圆C交于M,N两点,设直线OM,ON(O为坐标原点)的斜率分别为k1,k2,若对任意k,存在实数λ,使得k1+ k2=λk,求实数λ的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线C:![]() 的焦点为F,抛物线C与直线l1:
的焦点为F,抛物线C与直线l1:![]() 的一个交点为
的一个交点为![]() ,且
,且![]() (
(![]() 为坐标原点).
为坐标原点).
(Ⅰ)求抛物线C的方程;
(II)不过原点的直线l2与l1垂直,且与抛物线交于不同的两点A,B,若线段AB的中点为P,且|OP|=|PB|,求△FAB的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】2017年是某市大力推进居民生活垃圾分类的关键一年,有关部门为宣传垃圾分类知识,面向该市市民进行了一次“垃圾分类知识”的网络问卷调查,每位市民仅有一次参与机会,通过抽样,得到参与问卷调查中的1000人的得分数据,其频率分布直方图如图所示:
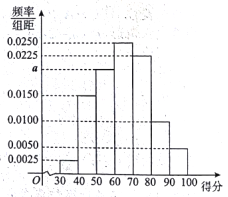
(Ⅰ)估计该组数据的中位数、众数;
(Ⅱ)由频率分布直方图可以认为,此次问卷调查的得分Z服从正态分布N(μ,210),μ近似为这1000人得分的平均值(同一组数据用该区间的中点值作代表),利用该正态分布,求P(50.5<Z<94);
(Ⅲ)在(Ⅱ)的条件下,有关部门为此次参加问卷调査的市民制定如下奖励方案:
(i)得分不低于μ可获赠2次随机话费,得分低于μ则只有1次;
(ii)每次赠送的随机话费和对应概率如下:
赠送话费(单元:元) | 10 | 20 |
概率 |
|
|
现有一位市民要参加此次问卷调查,记X(单位:元)为该市民参加.问卷调查获赠的话费,求X的分布列和数学期望.
附: ![]() ,
,
若ZN(μ,σ2),则P(μ-σ<Z<μ+σ)= 0.6826,P(μ-2σ<Z<μ+2σ)=0.9544.
查看答案和解析>>
科目: 来源: 题型:
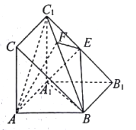
【题目】如图,直三棱柱ABC—A1B1C1中,侧面AA1B1B是正方形,AC丄侧面AA1B1B,AC=AB,点E是B1C1的中点.
(Ⅰ)求证:C1A∥平面EBA1;
(Ⅱ)若EF丄BC1,垂足为F,求二面角B—AF—A1的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】《九章算术》第三章“衰分”介绍了比例分配问题,“衰分”是按比例递减分配的意思,通常称递减的比例为“衰分比”.如:已知![]() 三人分配奖金的衰分比为
三人分配奖金的衰分比为![]() ,若
,若![]() 分得奖金1000元,则
分得奖金1000元,则![]() 所分得奖金分别为900元和810元.某科研所四位技术人员甲、乙、丙、丁攻关成功,共获得奖金59040元,若甲、乙、丙、丁按照一定的“衰分比”分配奖金,且甲与丙共获得奖金32800元,则“衰分比”与丙所获得的奖金分别为( )
所分得奖金分别为900元和810元.某科研所四位技术人员甲、乙、丙、丁攻关成功,共获得奖金59040元,若甲、乙、丙、丁按照一定的“衰分比”分配奖金,且甲与丙共获得奖金32800元,则“衰分比”与丙所获得的奖金分别为( )
A.![]() ,12800元B.
,12800元B.![]() ,12800元
,12800元
C.![]() ,10240元D.
,10240元D.![]() ,10240元
,10240元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com