【题目】树立和践行“绿水青山就是金山银山，坚持人与自然和谐共生”的理念越来越深入人心，已形成了全民自觉参与，造福百姓的良性循环．据此，某网站推出了关于生态文明建设进展情况的调查，现从参与调查的人群中随机选出20人的样本，并将这20人按年龄分组：第1组，第2组，第3组，第4组，第5组，得到的频率分布直方图如图所示

（1）求a的值．

（2）根据频率分布直方图，估计参与调查人群的样本数据的分位数（保留两位小数）．

（3）若从年龄在的人中随机抽取两位，求两人恰有一人的年龄在内的概率．

（I）求曲线y=f（x）在点x=处的切线的斜率；

（II）判断方程f '（x）=0（f '（x）为f（x）的导数）在区间（0，1）内的根的个数，说明理由；

（III）若函数F（x）=xsinx+cosx+ax在区间（0，1）内有且只有一个极值点，求a的取值范围.

（1）根据以上数据，能否有60%的把握认为“微信控”与“性别”有关？

（2）现从参与调查的女性用户中按分层抽样的方法选出5人赠送营养面膜1份，求所抽取的5人中“微信控”和“非微信控”的人数；

（3）从（2）中抽选取的5人中再随机抽取3人赠送价值200元的护肤品套装，记这3人中“微信控”的人数为X，试求X的分布列及数学期望及方差．

参考公式：，其中n=a+b+c+d．

【题目】已知椭圆的一个焦点坐标为．

（Ⅰ）求椭圆的方程；

（Ⅱ）已知点，过点的直线（与轴不重合）与椭圆交于两点，直线与直线相交于点，试证明：直线与轴平行．

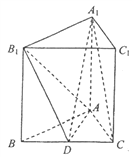
（I）求证：平面AB1D⊥平面BB1C1C；

（II）求证：A1C∥平面AB1D；

（III）求三棱锥A1-AB1D的体积.

(1)若小王发放5元的红包2个，求甲恰得1个的概率；

(2)若小王发放3个红包，其中5元的2个，10元的1个,记乙所得红包的总钱数为X，求X的分布列．

（I）求数列{an}的通项公式；

（II）求a2+ a4+ a6+…+ a2n.

【题目】已知正项数列的前项和为，数列满足．

（1）求数列的通项公式；

（2）数列满足，它的前项和为，

（ⅰ）求；

（ⅱ）若存在正整数，使不等式成立，求实数的取值范围．

（I）求f（x）的最小正周期；

（II）求证：当x∈[0， ]时，f（x）≥0.