
科目: 来源: 题型:
【题目】某城镇社区为了丰富辖区内广大居民的业余文化生活,创建了社区“文化丹青”大型活动场所,配备了各种文化娱乐活动所需要的设施,让广大居民健康生活、积极向上.社区最近四年内在“文化丹青”上的投资金额统计数据如表:(为了便于计算,把2015年简记为5,其余以此类推)
年份 | 5 | 6 | 7 | 8 |
投资金额 | 15 | 17 | 21 | 27 |
(1)利用所给数据,求出投资金额![]() 与年份
与年份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(2)预测该社区在2019年在“文化丹青”上的投资金额.
(附:对于一组数据![]() ,
, ![]() ,…,
,…, ![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为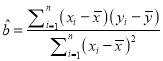 ,
, ![]() .)
.)
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场在一部向下运行的手扶电梯终点的正上方竖直悬挂一幅广告画.如图,该电梯的高AB为4米,它所占水平地面的长AC为8米.该广告画最高点E到地面的距离为10.5米,最低点D到地面的距离6.5米.假设某人的眼睛到脚底的距离MN为1.5米,他竖直站在此电梯上观看DE的视角为θ.
(1)设此人到直线EC的距离为x米,试用x表示点M到地面的距离;
(2)此人到直线EC的距离为多少米时,视角θ最大?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在边长为2的正方形ABCD中,P为CD中点,分别将△PAD, △PBC沿 PA,PB所在直线折叠,使点C与点D重合于点O,如图2.在三棱锥P-OAB中,E为 PB中点.
(Ⅰ)求证:PO⊥AB;
(II)求直线BP与平面POA所成角的正弦值;
(Ⅲ)求二面角P-AO-E的大小.

查看答案和解析>>
科目: 来源: 题型:
【题目】某人在塔的正东方向沿着南偏西60°的方向前进40 m以后,望见塔在东北方向上,若沿途测得塔的最大仰角为30°,则塔高为________________m.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知三棱锥![]() (如图1)的平面展开图(如图2)中,四边形
(如图1)的平面展开图(如图2)中,四边形![]() 为边长为
为边长为![]() 的正方形,△ABE和△BCF均为正三角形,在三棱锥
的正方形,△ABE和△BCF均为正三角形,在三棱锥![]() 中:
中:
(I)证明:平面![]()
![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)若点![]() 在棱
在棱![]() 上,满足
上,满足![]() ,
, ![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() ,求
,求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目: 来源: 题型:
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+![]() )(A>0,ω>0,|
)(A>0,ω>0,|![]() |<
|<![]() )在某一个周期内的图象时,列表并填入了部分数据,如表:
)在某一个周期内的图象时,列表并填入了部分数据,如表:
ωx+ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+ | 0 | 5 | -5 | 0 |
(1)请将上表数据补充完整,并求出函数f(x)的解析式;
(2)将y=f(x)的图象向左平移![]() 个单位,得到函数y=g(x)的图象.若关于x的方程g(x)-m=0在区间[0,
个单位,得到函数y=g(x)的图象.若关于x的方程g(x)-m=0在区间[0,![]() ]上有两个不同的解,求实数m的取值范围.
]上有两个不同的解,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com