
科目: 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() ,侧面
,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
, ![]() 分别为
分别为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)如果直线![]() 与平面
与平面![]() 所成的角和直线
所成的角和直线![]() 与平面
与平面![]() 所成的角相等,求
所成的角相等,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】2016年1月1日,我国实行全面二孩政策,同时也对妇幼保健工作提出了更高的要求.某城市实行网格化管理,该市妇联在网格1与网格2两个区域内随机抽取12个刚满8个月的婴儿的体重信息,体重分布数据的茎叶图如图所示(单位:斤,2斤![]() 1千克),体重不超过
1千克),体重不超过![]() 千克的为合格.
千克的为合格.

(1)从网格1与网格2分别随机抽取2个婴儿,求网格1至少有一个婴儿体重合格且网格2至少有一个婴儿体重合格的概率;
(2)妇联从网格1内8个婴儿中随机抽取4个进行抽检,若至少2个婴儿合格,则抽检通过,若至少3个合格,则抽检为良好,求网格1在抽检通过的条件下,获得抽检为良好的概率;
(3)若从网格1与网格2内12个婴儿中随机抽取2个,用![]() 表示网格2内婴儿的个数,求
表示网格2内婴儿的个数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列叙述中正确的是( )
A.若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;
B.若三个平面两两相交,其中两个平面的交线与第三个平面平行.则另外两条交线平行;
C.如果![]() 是两条异面直线,那么直线
是两条异面直线,那么直线![]() 一定是异面直线;
一定是异面直线;
D.在![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]() 绕
绕![]() 所在直线旋转一周,所形成的几何体的轴截面面积为10.
所在直线旋转一周,所形成的几何体的轴截面面积为10.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)求直线![]() 的标准参数方程;
的标准参数方程;
(2)求![]() 的长;
的长;
(3)以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,设点
轴的正半轴为极轴建立极坐标系,设点![]() 的极坐标为
的极坐标为![]() ;求点
;求点![]() 到线段
到线段![]() 中点
中点![]() 的距离.
的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图半圆![]() 的直径为4,
的直径为4,![]() 为直径
为直径![]() 延长线上一点,且
延长线上一点,且![]() ,
,![]() 为半圆周上任一点,以
为半圆周上任一点,以![]() 为边作等边
为边作等边![]() (
(![]() 、
、![]() 、
、![]() 按顺时针方向排列)
按顺时针方向排列)
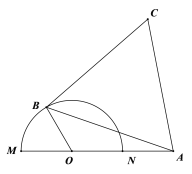
(1)若等边![]() 边长为
边长为![]() ,
,![]() ,试写出
,试写出![]() 关于
关于![]() 的函数关系;
的函数关系;
(2)问![]() 为多少时,四边形
为多少时,四边形![]() 的面积最大?这个最大面积为多少?
的面积最大?这个最大面积为多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PD⊥平面ABCD,![]() ,∠ABC=∠BCD=90°,E为PB的中点。
,∠ABC=∠BCD=90°,E为PB的中点。

(1)证明:CE∥面PAD.
(2)若直线CE与底面ABCD所成的角为45°,求四棱锥P-ABCD的体积。
查看答案和解析>>
科目: 来源: 题型:
【题目】某地植被面积 ![]() (公顷)与当地气温下降的度数
(公顷)与当地气温下降的度数![]() (
(![]() )之间有如下的对应数据:
)之间有如下的对应数据:
| 20 | 40 | 50 | 60 | 80 |
| 3 | 4 | 4 | 4 | 5 |
(1)请用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据(1)中所求线性回归方程,如果植被面积为200公顷,那么下降的气温大约是多少![]() ?
?
参考公式:用最小二乘法求线性回归方程系数公式: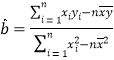 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,且
为参数,且![]() ),以
),以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,建立极坐标系,直线
轴的正半轴为极轴,建立极坐标系,直线 ![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若曲线![]() 与
与![]() 只有一个公共点,求
只有一个公共点,求![]() 的值;
的值;
(2)![]() ,
, ![]() 为曲线
为曲线![]() 上的两点,且
上的两点,且![]() ,求△
,求△![]() 的面积最大值.
的面积最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com